Explore

Choose country

A direct test of the flat earth model: flight times

More data supporting a spherical earth

by

Published: 6 December 2016 (GMT+10)
Flat Earth Society, with annotations by RC flat-earth
Figure 1: “Flat earth” map obtained from the Flat Earth Society website. The locations of the cities used in this study are marked (blue dots), as are the straight-line distances from Johannesburg to each city (red lines). I also added a black flag at the approximate position of the north pole. Originally, the city locations were marked in pen on a printed copy of this map, using various geographic hints from the map itself, but the data are recreated here for the sake of the reader.

After receiving such a surprising number of negative comments on our flat-earth rebuttal, I decided to perform a numerical analysis of the flat-earth model compared to the traditional spherical-earth model.

Science is about testing hypotheses, so let us set up an experiment to test these alternative views. For this, I enlisted the help of two of my children, ages 13 and 11. It made for a fun homeschool project.

The basic problem is the distance between longitude lines in the flat-earth model. In a spherical earth, the longitude lines start from one pole and converge on the other pole, and the distances get wider the closer they are to the equator. But in the northern-hemisphere–biased flat-earth model, the longitude lines start from the north pole and radiate outwards to the supposed ‘encircling southern polar ring’ like spokes on a wheel.

This means that the distances become greater the further south they go. This suggests an easy test of the two models: compare distances to travel times for distant places in the southern hemisphere.

The goal of this simple study was to compare reported airline flight time data with two distance measures, the ‘great circle’ distance of spherical-earth theory and the ‘straight-line’ distance of flat-earth theory.

The driving hypothesis is that the flat-earth map is distorted and so the flight times will not match the calculated distances. This, of course, assumes there is no great conspiracy among the millions of people working for the airline industry or the tens of millions of people who fly on their airplanes annually, which seems reasonable. I am also assuming airplanes on a flat earth would use the rule we all learned in geometry that ‘the shortest distance between any two points on a [standard, Euclidean] plane is a straight line’.

This assumption was in favor of the flat earth model for, as we will see, any curved line would only exacerbate the noticeable distortion with increasing flight time and distance from the source.

Flat_Earth_Figure_2
Figure 2: Measured string length vs. great circle distances.

First, I obtained a map from the Flat Earth Society website (figure 1). With the help of one of my daughters, we located a suitable city that had many non-stop flights to different cities on other continents. In this case, we chose Johannesburg, South Africa.

We then looked up flights from this city and chose representative destinations on every continent (table 1). After carefully marking the city locations on a printed copy of the map, we painstakingly measured the distances between the cities using a ruler, to the nearest millimeter.

Table 1: Flight data from Johannesburg. Flight times and (great circle) distances were obtained from various online databases and calculators. Physical distances were measured on a globe using a taut string (to the nearest half-cm) and on the flat-earth map using a ruler (to the nearest mm). The globe was approximately 42 cm in diameter. The map was printed to the extents of an 8 ½ x 11 in. sheet of paper. Negative latitudes are south of the equator. Negative longitudes are west of the Prime Meridian.

CityAirport
Code		LatitudeLongitudeFlight Time
(hrs)		Distance
(km)		Measured Distances
String (cm)Flat (cm)
Johannesburg JNB -26.134 28.242 -- -- -- --
Antananarivo TNR -18.797 47.479 3.2 2,156 6.5 3.2
Mahé SEZ -4.674 55.522 4.9 3,752 12.0 4.2
Dubai DXB 25.253 55.364 8.1 6,389 20.5 4.9
Dakar DKR 14.740 -17.490 8.5 6,705 21.5 5.6
Tel Aviv TLV 32.011 34.887 9.1 6,473 20.5 4.4
Perth PER -31.940 115.967 9.2 8,326 26.0 12.4
Istanbul IST 40.976 28.814 9.5 7,430 24.5 5.0
São Paulo GRU -23.382 -46.469 9.8 7,451 23.5 9.9
Madrid MAD 40.494 -3.567 10.3 8,077 26.0 5.7
Singapore SIN 1.359 103.989 10.4 8,661 27.5 9.7
Frankfurt FRA 50.033 8.571 10.8 8,658 27.5 5.9
Zurich ZRH 47.465 8.549 10.8 8,387 27.5 5.6
Amsterdam AMS 52.309 4.764 11.1 8,986 29.0 6.1
London LGW 51.148 -0.190 11.3 9,004 29.0 6.2
Sydney SYD -33.946 151.177 11.8 11,044 35.0 15.8
Hong Kong HKG 22.309 113.915 12.8 10,672 34.5 9.8
Beijing PEK 40.067 116.600 14.1 11,699 37.5 9.5
New York JFK 40.640 -73.779 15.8 12,824 41.0 9.9
Atlanta ATL 33.637 -84.428 16.4 13,581 44.0 10.6

Next, with the help of my son, we went to the local library because we knew they had a medium-sized globe (approximately 42 cm diameter). We could have simply used the great-circle calculations from table 1, but I felt it was more fair to use my own measurements since I was manually measuring the flat-earth distances. Plus the more error we added, the more difficult it would be to conclude one method was less accurate than the other. It was highly likely that my rudimentary string-on-a-globe method would be wildly inaccurate.

Taking a string, he held the end on Johannesburg while I attempted to make a great-circle to each city. Together, we measured the length of the string from the end to the point where I had pinched it, to the nearest half-cm. This level of precision was chosen so that it did not exceed that of the flat-earth measurements. I wanted to make sure there was a higher level of precision in the theory I do not support. I did not expect much success, and was surprised after I plotted the distances obtained from my string method vs. the great circle distances in table 1 and obtained a line of best fit with an R2 (correlation coefficient) greater than 0.99 (figure 2). According to the string lengths, the scale of the globe was about 313 km/cm.

Flat_Earth_Figure_3
Figure 3: Reported great circle distances vs. reported flight times.

The final step was to compare the spherical-earth and flat-earth distances with flight times. First, I graphed the great circle flight distances vs. the flight times I obtained from the internet. Given that we are dealing with different airlines, airplane models, airport approaches, and taxiing times, I expected to see more variability in the data. However, a straight-line approximation was obtained, with an R2 greater than 0.97 (figure 3).

This set a high standard for the flat-earth model to meet. The average speed (the slope of the line of best fit) was 871 km/hr, which is a good approximation of the average speed of a modern airliner. The modern long-distance commercial airplane is designed to cruise efficiently at around mach 0.8, with speeds depending on altitude, airplane type, and the speed of local air traffic. Thus, the reported great circle distances are an excellent estimation of the expected flight time. This is another high bar for the flat-earth theory to hurdle.

The next step was to add a comparison of flight speed vs. distance in the flat-earth model, but the data are not in the same units. In fact I had three different units with which to contend: km/hr, cm/hr on the globe, and cm/hr on the flat map. Yet, the solution to this dilemma is simple. The measured distances had to be normalized by dividing by the shortest distance in each dataset.

Flat_Earth_Figure_4
Figure 4: Normalized distance data vs. reported flight times. The line of best fit is given for the string-length data and the flat-earth data. The string-length data are slightly below the corresponding great circle data, indicating that the shortest string-distance measurement was slightly off (+0.5 cm). Note the highly significant correlation between the string-length data and reported flight times (R2 = 0.9762). Note also the lack of correlation between the flat-earth distance data and flight time (R2 = 0.3388). The cities that were farthest off the line in the flat-earth model are the cities with the greatest longitudinal (spherical earth model) difference from Johannesburg.

The normalized data revealed a tight correlation between the spherical earth model and flight time, but no apparent correlation was seen between the flat-earth model and flight time (figure 4). The flat-earth data are so bad that no additional statistical measures were warranted. There is simply no correlation, and the data points that are closest to being true are also the ones closest to the same longitude (i.e. the distances are not distorted by the flattening of the truly spherical earth onto the flat projection).

One might think that, since the normalized flat-earth data are generally below the others in figure 4, that the distances between these cities are shorter in the flat-earth model. However, the normalization process is entirely dependent on the shortest measured distance (in this case, Johannesburg to Antananarivo) and any distortion within the map projection will affect all data points. Since Madagascar is due east of southern Africa, and since both are at a relatively high latitude, the flat-earth projection artificially inflates the true distance.

Comparing the normalized flat-earth distance data to the city list in table 1 demonstrates that the cites with the greatest deviation from expected are the ones that are the farthest east and west of Johannesburg, namely Sydney, Perth, São Paulo, Singapore, and Hong Kong, in decreasing order.

Also, for any group of cities that are more or less along the same straight line from Johannesburg, the closer cities display less error than the farther ones. This is yet another example of the unreality of the flat-earth projection.

One additional measure is the string-length/flat-earth distance ratio. This will tell you proportionally how far apart the two distance measures are and it varies from 2.03 (Antananarivo) to 4.91 (Zurich). In this case, the ratio is highest for the cities in Europe and other places directly above southern Africa on the map, and lowest for cities farthest to the left and right. In fact, the angles of the lines in figure 1 are a direct estimate of this ratio. In other words, the flat map is distorting the true distances in a predictable manner.

Looking out the window

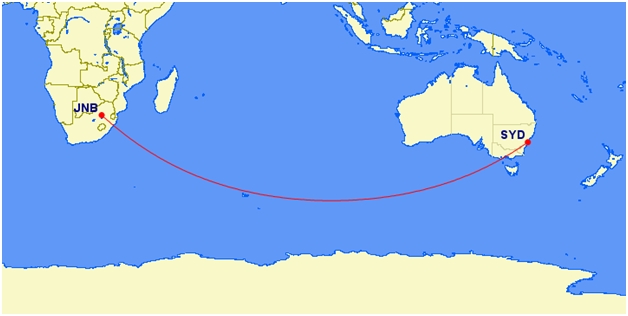
Unless we think all the flight times are wrong and the thousands of passengers are also lying about them, planes would have to be supersonic and have much greater fuel capacity than they do to make many of these routes. Also, the geography of the great circle routes on a global earth is very different from that of the straight-line routes on a flat disk. Passengers on multiple different flights would report seeing very different things out the window if the earth was flat.

For example, passengers on the Johannesburg to Sydney flight have fairly monotonous scenery for nearly the entire trip: the southern Indian Ocean. On a flat earth, the flight would go over the Himalayas (which would be hard to miss!) and other land.

Great Circle Mapper © 1996-2016 Karl L. Swartz, gcmap.com Flat_Earth_Figure_5
Figure 5: The great circle route from Johannesburg to Sydney crosses the southern Indian Ocean, as reported by many eyewitnesses who have flown this route. It does NOT cross the Himalayas as it would in the flat-earth model (figure 1). 

Conclusions

I have set up a simple experiment to test two alternative models of reality. The spherical-earth model came through unscathed. The flat-earth model simply fails to reflect reality. I even made simplifying assumptions in favor of the flat-earth.

Anyone reading this has but two choices: either accept this experimental evidence or reject the reported flight times. However, if you are toying with the latter, please consider that these are backed up by the personal experiences of millions of people and the economic needs of billion-dollar companies in a cut-throat industry where the smallest profit margin might make or break a company.

If you conclude that the flight time data are inaccurate (and they have to be very much so), you are rejecting the type of data upon which your entire society is based. You could not use a computer, drive a car, or read this internet article if this logic upon which this study is based is not real.

If you still want to retreat into the flat-earth position, you are neither siding with the near-unanimous conclusions of 2,000 years of Christian scholarship, the biblical text when properly placed in its grammatical and historical perspective, abundant and simple experimental science, or logic.

Thus, you have not a leg to stand on. Please consider your answer carefully! Also consider that I have not just thrown up a list of facts that supposedly support my own pet theory. I took a lot of time to actually analyze real data. Have you ever seen a flat-earth document that even attempted this level of analysis? No, I didn’t think so.

Related Articles

Further Reading

Helpful Resources

Readers’ comments

Mike S.
GB December 18th, 2016
Dear Dr. Carter, once again I commend you and the staff at CMI. How patient, gracious and loving to supply us 'lesser mortals' with such resources to help refute this very strange myth. So sad, we have family members we love very much appearing to believe and promote the FEM. And they seem unable or unwilling to examine the evidence you provide. We seem unable to reach them, but pray on that our Lord will be merciful and open their eyes. We could not have made the attempts we have without your articles to inform us. Thank you again and may God bless your ministry mightily.
Robert Carter
December 19th, 2016
Thank you for those words of affirmation. It is difficult to write articles like this, and even more difficult to deal with the reactions we receive from certain quarters. However, knowing there are people like you that are benefited by our efforts makes everything worth while.
Edwin W.
CA December 13th, 2016
First of all, the math: The official geodetic mensuration reference is NATIONAL IMAGERY AND MAPPING AGENCY TECHNICAL REPORT 8350.2 Third Edition. The (alleged) mean radius or Mean Radius of Semi-axes, R1, of the Earth is 6371008.7714 meters. The amount of (alleged) vertical drop based on the (alleged) radius of the Earth is simply y = R1 {1 – [cos (s/C) x 360°]}. The distance to the horizon s (in statute miles) is C arccos [1 – (E / R1)] / 360⁰, where E is the relative elevation. The effective distance below the horizon, i.e., y’, when the elevation, h, of the observer or optical instrument relative to the observed island, promontory or structure is considered is y’ = R1 x (1 – cos {[(s/C) x 360⁰] – arccos [1 – (E/R1)]}). Secondly, the geographical locations: The observation was made from a 50-foot coastal bank above Murphy’s Pond, NS; the geographical coordinates are 46.028640, -61.548361. What I observed was the coastline near Souris, PE; the geographical are 46.354980, -62.251834. The computed distance is 40 statute miles. Using a table constructed in Excel from the above formula, the shoreline at Souris should have been 655 below the horizon. [That previous refraction factor of 4/3 is too conservative as it applies to radar propagation; the refraction factor for optical propagation is actually about 7/6 or 1.15 – see Newsome, Weather Radar Networking Cost Project 73.] The above formula using the effective earth radius of 1.15x dictates that the Souris shoreline should be 547 feet below the horizon. The online topographic survey of Canada indicates a maximum elevation of 50 meters (or 164.042 feet) in the extreme eastern part of Prince Edward Island). The highest elevations in the Souris area should be about 383 below the horizon.
I again rest my case.
Robert Carter
December 14th, 2016
Dear creation.com readers. This is the third post from this person. In reply to his last comment, I said his math was atrocious and that all such examples fall when carefully scrutinized. He fired back with this dizzying array of signs and numbers.

How do react when you see thing like this? The person is convinced of his opinion, seems to have data to back up his claims, speaks authoritatively, and throws around mathematical formulae like he knows what he is doing. Seriously, how do you react when you see something like this? Presentations like this are intimidating, but take heart! It usually does not take much digging to solve the riddle, as is true in this case.

For the record, I was referring to his claim that "Atmospheric refraction increases the effective radius of the allegedly spheroidal earth by approximately 4/3 (the k-factor)" when I said 'his math was atrocious'. I should have been more clear and did not mean to mislead anyone or to cast aspersions on his grasp of trigonometry. Since I made that small mistake, I felt I should take some time to answer his mathematical treatise. I did not have to do so and probably will not respond to anything else he posts, but here goes nothing:

First, I got on GoogleEarth and looked up his locations. Indeed, there is about 38 miles (62 km) between these points and the elevations are about what he claimed. I am going to assume he did his calculations correctly but I know that over 40 miles there is enough curvature to hide one location from the other. So, is he right? Should it be impossible to see Souris, PE from Murphy's Pond, NS?

First, note that nearly all such claims involve looking across water. This phenomenon has been known for centuries and atmospheric refraction is the culprit. Ignore his "4/3" rule, for it is certainly being misapplied. All it would take to validate his claims would be to take sightings of various landforms from multiple places simultaneously and apply some triangulation. If you can see point A from point B, how do things look from point C, or point D?

But you don't even have to do that (although it would be fun). Just search the Internet for "Crocker Land". There are two historical examples. The first was from the early 1800s that caused a ship to return from searching for the Northwest Passage when the captain saw high mountains (subsequently named Crocker Land) blocking his path in the distance. Problem is, there are no mountains in that direction (from a point west of NW Greenland). The second example is from another Arctic expedition about a hundred years later that tried to reach Crocker Land, which was easily and clearly seen by them. They traveled across the ice for more than 100 miles, and were forced to conclude that they were indeed seeing something that was not there. They were probably seeing a fata morgana (a type of mirage) created by a combination of the cold but crystal clear air and the extensive sea ice that stretched for miles beyond the horizon.

There are many, many examples of such things from history, from all over the world. But when they are seen, they DO NOT FIT the flat earth model. First, the size of the image is not commensurate with the distance. In fact, the image is the size it should be if the object were much closer that it really is. It is as if you are seeing the object from a closer vantage point. Second, the images are illusory. They can waver, flip over, disappear, reappear, all in the matter of a few minutes. Third, they are not visible under all clear-sight conditions. In fact, it takes a specific set of atmospheric conditions to produce them. Thus, very often you cannot see them even on the clearest days, which should not be true if the earth was indeed flat!

See the image of Toronto in our main article. Notice that you cannot see the base of the tall buildings because they are hidden by the curve of the earth. The same is true of many mirages. As I said above, you are seeing an image that appears closer than it should. Why? Because the light rays bend as they travel through air layers of different temperatures. This causes the light that should be striking in one place to instead strike in another. In cases like this, you are seeing the image as it would be if seen from a closer vantage point.

I must thank Edwin for the comments. He caused lots of discussion here in the office and gave me a chance to read up on some fascinating science, some of which I knew, some of which I had forgotten, and some of which I learned while writing out this answer. If nothing else, his attempted rebuttal has given me (and hopefully you) a better ability to decisively answer the flat earth belief.
Edwin W.
CA December 12th, 2016
Atmospheric refraction increases the effective radius of the allegedly spheroidal earth by approximately 4/3 (the k-factor). That factor is woefully insufficient to account for what everyday people are seeing worldwide, not to mention routine optical and radar observations by military personnel and air traffic controllers who actually have to perform safety-critical functions in the real world – as it is – not as it is advertised. In my own geographic region, I am able to view (on a clear day) an island 40 statute miles distant from a height of 50 feet above sea level. Based on WGS84, the shoreline of that island should be 655 feet below the horizon. If refraction is factored into the calculation, the shoreline of that island should still be 450 feet below the horizon. The maximum elevation of the island is about 165 feet. So even the top of the island’s landscape should be 285 feet below the horizon. But almost the entire vertical profile of the landscape is visible when viewed with the Nikon Coolpix P900. I rest my case.
Robert Carter
December 12th, 2016
Readers beware! His math is atrocious. His claims are false. Do not be misled by cases like this. Atmospheric refraction is the answer to all of these "we can see stuff that should be below the horizon" claims. That is, those claims that are not specious. I am not going to bother double checking, but how could I anyway since he provided no geographic details? These arguments only have the appearance of truth and they fall quickly when scrutinized.

However, so what? As a scientist, I could never "rest my case" with one bit of 'evidence' like this. There are always apparent contradictions in science and all scientific positions must wrestle with contravening data. In this article, I presented a conclusive rebuttal of the flat earth, and we presented more details in the original article, but he wants to ignore this information because he 'can see stuff below the horizon'.

Here's how this works: Position 1 (flat earth) attempts to explain the line-of-sight anomaly by saying the earth is flat, but they must reject the published flight schedules of the cutthroat, billion-dollar airline industry and the testimony of tens of thousands of airline passengers and employees. Position 2 (spherical earth) can explain BOTH the line-of-sight anomaly and the airline flight data. The testimonies of the thousands of people involved only confirm the model. Who do you think wins in this case?
Edwin W.
CA December 12th, 2016
You have not carried out a scientific experiment because you have presented flight data that is necessarily outside the scope of your direct, empirical verification. You have simply carried out an analysis of information and data that you have taken without question from the public domain. Hence, you have not concluded anything scientifically. The flat earth researchers on the other hand easily disprove the alleged curvature of the earth by reporting direct and repeatable observations of islands, promontories and structures that would otherwise be impossible to see based upon the mensuration associated with World Geodetic System 1984. I continue to be amazed at why so many creation researchers dismiss modern day confirmation of the terrestrial plane – a confirmation that subsumes fiat creation and vanquishes evolutionism once and for all. Perhaps it is a naïveté that the rabbit hole of deception cannot possibly be that deep. I wish that were true.
Robert Carter
December 12th, 2016
Edwin, your definition of 'science' is wanting. I did not just take information out of the pubic domain, I myself have verified some of the published flight information, including routes and flight times between LA and Shanghai, LA and Taiwan, Taiwan and Bali, LA and Brisbane, LA and Sydney, LA and Auckland, Orlando and London, NY and Hamburg...shall I continue? In a reply to a recent comment, I also verified the South Africa to Australia data presented in the table above by accumulating testimonies from three other CMI speakers.

But I don't even have to verify the data. If the data the airlines publish are not accurate, they would have gone bankrupt a long time ago. Some in your community want to say these flights do not actually exist. One of the recent commentators even said he 'wanted to meet that person' who had taken the flight in question, yet here we are. It would be impossible to create a conspiracy of this scale and nature, and it would be impossible to maintain it in the face of so many confirming witnesses.

You claim that the flatness can be seen observationally? But we know the atmospheric conditions that allow for seeing things that would not otherwise be along the line of sight. It is called refraction. I would encourage you to look it up, but you obviously either have not read the article(s) or are unwilling to actually engage your brain. Both sides claim to explain this phenomenon, thus it is in no way proof of one side over the other. You need to read How to think, not what to think.

The weight of evidence is so strongly against you that you actually have no theory. All you can claim is "conspiracy" and "people are lying" and things like that. And you claim I do not understand science! Please, pop your head out of "the rabbit hole of deception" and take a look around.
Judie S.
AU December 9th, 2016
The death of John Glenn this week should remind us all of the huge number of Christian astronauts who must also be lying when they speak (and take photographs) of the globe.
Robert Carter
December 9th, 2016
This is an excellent point, and one which we have made several times in our anti-flat earth and anti-geocentrism articles. We would have liked for John to have accepted Genesis as history and to have rejected deep time and evolution. It is also a shame that he supported partial birth abortion and in general had a pro-abort voting record and strongly pushed for taxpayer funding of abortions at military bases. But he at least accepted the basic tenets of Christianity (i.e., Christ's miraculous birth, his substitutionary death, and his resurrection) and seemed to have led a faithful life and was not bashful about his faith.
The 8th and 10th men to walk on the moon, Jim Irwin and Charlie Duke, later became Genesis-believing Christians. If any reader is looking for a rocket scientist with a deeper commitment to Genesis, see our interview with Dr. Henry Richter.
Joe B.
US December 9th, 2016
I love real science, that is, science that is supported by experiments and experimental observation. I have read lots of stuff on both sides of the Creation-Evolution debate and have to say the CMI rates at or near the top of the objectivity list! May the Lord continue to direct your steps in getting out the truth that the Lord is God AND Creator of all things. Here is just a little jab at the flat-earth community. Answer this: why does the Lord describe separating our sins from us as far as the east is from the west in Psalm 103? Why not the north from the south? Well, its because the north and south are nodes that are a finite distance apart that can be reached by traveling in that direction until you get there. But travel east and you will continue to go east forever, travel west and you will continue to travel west forever!-)
Sam H.
US December 8th, 2016
It really made me sad when I read your first article on "flat earth". Imagine how disappointed I was when I read another. Not because I think the earth is flat, but because it is somehow a topic that would even warrant an article about it. My brain cannot fathom how people can honestly believe the world is flat. To what end? Christians who believe such a theory are putting all of us back nearly 1000 years. Non-Christians who see Christians believing in something as scientifically trivial as flat vs spherical earth will never bother trying to even check the facts about a much more important topic such as evolution.

As always...Thank you, CMI.
Robert Carter
December 8th, 2016
Makes me sad, too. And thank you for your support. One small correction, though. In one sense they are setting us back 1000 years to the place where people could believe that some church had a fragment of the "true cross", and things like that, with no empirical evidence to support such a claim. In another sense they are not setting us back 1000 years, since there is no evidence that anybody back then thought the earth is flat. Instead, they are jettisoning the Christian tradition along with common sense. Thus, the flat earth idea is worse than most people think.
Colin N.
AU December 8th, 2016
Robert Carter, I think you misunderstood my post. The FE group acknowledges that there are both a summer and a winter. In the summer according to them, the sun circles closer to the Northern pole or whatever they call it and in the winter, closer to the edge of the Earth, thus necessarily covering a much greater distance (a larger circle). Therefore the sun must cover a much greater distance in the same amount of time in the latter circuit (if they are correct). This calls for the sun to both speed up and slow down in its circuits if the days are to remain similar in timing.
Robert Carter
December 8th, 2016
Thank you for clarifying what you meant (you said nothing about summer and winter in the original post). In this you are 100% correct and have hit upon yet another problem with their idea. However, since nothing in their model depends upon physics, I predict they will just say, "The sun slows up and speeds down. So what?" To this we will have to reply, "Yeah, but we can measure the speed of the sun across the ground and it does not match the requirements of your model. It does, however, match Kepler's laws." Etc.
Vernon R.
US December 8th, 2016
I am not a believer in a flat earth in any way, but I had an interesting experience as a young Marine going home from Vietnam. We left DaNang on a Boeing 707 to Okinawa, from there we flew non stop to Oakland, California where the plane ran out of fuel just before we touched down on the runway. We continued to El Toro Marine air base where we checked in to customs then went to LAX and from there to home in the desert southwest. We left Okinawa at 12 noon on the 28th of July, I arrived at home at 11 AM on the 28th of July, one hour before I left Okinawa. Our course was along the eastern coast of Asia, then along the Aleutian's, down the coast of Alaska and Canada and the west coast of the U.S. Part of our flight was during the day time and from the window I was sitting by I could see what appeared to me to be the curvature of the earth. I know when I was aboard ships I could see the curve. I have always thought that Columbus voyage proved that the earth wasn't flat.
Robert Carter
December 8th, 2016
Thank you for your comment (and your service!). Your flight path is exactly that predicted by a great circle drawn on a globe between those two points. However, the idea that Columbus proved the earth is a sphere is not supported by history. Everybody believed the earth was a sphere, and if there was an argument it was that Columbus thought the earth was much smaller than it truly is, and was wrong. See The Flat Earth Myth.
Egil W.
NO December 7th, 2016
Contrary to what both liberal theologians and flat-earthers may think, the Bible no-where says the earth is flat. They should think about it, because it appears to me they are not aware of the actual difference between what the Bible explicitly claims and their own "reading-into-the-text-their-already-held-biases"; the difference between exegesis and eisegesis. The only difference between the liberal theologian and the flat-earther being the content of their bias, or the "authority" given to a bias; the liberal theologian - whatever the majority-consensus of contemporary science (which then becomes scientism), holds as true, while the flat-earther believes that whatever...NASA and majority-science says is always wrong and thus ends up believing the same as the liberal scholar; that the Bible has a babylonian worldview. To a flat-earther two or three poetic-styled Bible-verses read as literal narrative trumps a plain, well-studied, balanced reading of the entire Bible where all verses, all chapters, are read for precisely what they are given to say and all is taken into consideration. The first is then like the sadducees who just couldn´t believe, or have faith in anything supernatural, even if described by the Word of God, the latter becomes sectarian and overtly anti-social and worse still; completely unbalanced in the use of the Bible. In their attempt to never give any authority to the great conspiration "out there", they actually let a majority-consensus-science rule their bias...simply by squarely taking a stand against all-of-it; if NASA says so, its always wrong, so wrong that the oppsite is true...their worldview ends up being an inversion of whatever NASA says...the possibility of just diving into the subject-matter of the individual question eludes them.
Edgar N.
CA December 7th, 2016
The first challenge to the validity of your experiment is " which map did you use? " Even modern day maps are severely distorted as a current study clearly demonstrates. Take a look at a map today, and you’re likely to see that North America is larger than Africa, Alaska is larger than Mexico and China is smaller than Greenland. The map you use is critical to an accurate result and the best flat earth map to date is the flat Earth Azimuthal Equidistant map. An interesting story The Diverted Flat Earth Baby Flight and International Shipping. Although this Exhibit builds on the other exhibit discussing southern hemisphere flight patterns, this story most certainly fits the flat Earth model as it pertains to both hemispheres. In October 2015, a China Airlines flight from Bali to Los Angeles was diverted because a woman prematurely had her baby on the flight. A fun story but it also proves the flat Earth because the flight was strangely diverted to and made an emergency landing in Anchorage, Alaska. Get out your globe and you will see that there is no way that Anchorage, Alaska was anywhere near the route of the flight which could have just easily continued its path straight to Los Angeles or landed in Honolulu. However, on the flat Earth Azimuthal Equidistant Map (the same one that matches the UN flag), Anchorage, Alaska is very near the route. We are told that Earth is spinning around its axis at 1,000 miles per hour, revolving around the Sun at 67,000 miles per hour, while the entire solar system rotates around the Milky Way galaxy at 500,000 miles per hour. Or you can believe scripture 1 Chronicles 16:30 King James Version (KJV) Fear before him, all the earth: the world also shall be stable, that it be not moved.
Robert Carter
December 7th, 2016
Your challenge is baseless, for I did not use any map! Instead, I used a globe, which, because the earth is also a globe, has no distortion of landmasses. If you want to argue accuracy, you will have to argue that I should have used an oblate spheroid instead of a globe, but at the scales we are talking about the earth is so close to being a perfect sphere that it would not matter.

I also have flown from Bali to LA! The great circle route takes you about half-way between Hawaii and the Aleutian Islands. Problem is, my flight went through Hong Kong and THAT great circle takes you very close to Alaska. You are making a non-argument.

For Scriptural references, what do you do with the very same Hebrew word saying the Psalmist will not be moved? See this article for more explanation.
A. F.
NO December 7th, 2016
Good article. I did my own practical horizon experiment on this topic and came to the same result that the earth is non-flat.
[link deleted per feedback rules]
Steve B.
US December 7th, 2016
How can those who believe in a flat earth explain why the sun and moon always appear round from all points they're seen from the earth at any given time. The sun and moon would appear elliptical at some points and round at other points. Isn't it true that the only way the sun could appear round from all points it's seen from earth at any given time is the earth and sun must both be spherical.
P. C.
GB December 7th, 2016
I would like to add. Did you actually try to book any of the flites you looked at? I tried to book a Johannesburg to Sydney flight. that said direct. after trying to book it. I had to do one stop in Hamad International Airport. on the flat earth mad this is virtually on the way. if you know anyone who has taken this flight direct to Sydney I would be very happy to know them :) thanks!!
Robert Carter
December 7th, 2016
Nice try, but this isn't going to 'fly'. Think about this: you have contacted a multi-national ministry with offices in seven countries, including Australia and South Africa, both of which are in the "Commonwealth" [formerly "British Commonwealth"]. These two countries have a lot of communication between them. Do you think maybe that some of our speakers have made that flight? Actually, many have. A quick, non-scientific poll found three names -- 100% of the people I asked. They have also flown from other cities in Australia, and they can attest to the very boring trip over the south Indian Ocean -- NOT over land, as would be required on a flat earth.

You say you "tried" to book a flight. Did you really? Or are you just parroting what you have heard from other flat-earthers? Note also that due to the fact that most airlines have major hubs, not all carriers make the direct flight, nor are they expected to. Yet, maybe you should have tried flight QF63/QF64. That is a direct, non-stop, great-circle route that takes you right where it should if the earth were a globe. Here's a generic review (you'll have to ignore the statements about polar bears and chemtrails. It's obviously not written by a scientist!):

http://www.gotravelyourway.com/2013/07/20/qantas-flight-qf63-from-sydney-to-johannesburg/

Note to others: I easily found three CMI speakers that have made this exact and/or similar flights from Johannesburg to Australian cities. Flat-earthers attempt to claim that these flights do not actually exist. I can be adamant about this: they are not telling the truth.
Colin N.
AU December 6th, 2016
According to the imaginary Flat earth Model, the sun should take longer to cover the distance in the Southern (hemisphere) or section, than in the Northern because the distance should be far greater. Therefore the days should be much longer. What is the truth? Length of days in both hemispheres are the same.
Robert Carter
December 7th, 2016
According the the Flat Earth Society model, there is no northern or southern hemisphere. Instead, the sun circles above the flat, dinner plate-like earth more or less above the equator. The real problem is that the sun would not follow the observed path in the sky if it were circling above the earth at only a few thousand miles.
Mark S.
CA December 6th, 2016
Thank you for introducing your subscribers to the concept. For those of you new to this, get ready, because your world is about to change, and it's never going to be the same again. Everyone laughs at first, but when you're done, ask yourself this: When did you first find out you lived on a globe? Because of the model you saw when you were six, or because of the ONE picture you saw in a textbook. Do your own research, and ask questions.
Robert Carter
December 6th, 2016
You encouraged people to do their own research, yet why not start with the research I present in the article? Do you ignore anything that contradicts your theory? By introducing our readers to the concept in this way, we are inoculating them against this form of sophistry. And, by allowing our detractors to attempt a rebuttal, then answering them decisively, people can see who has the better theory. Fans of Creation.com will not be easy prey to the flat-earth farce.
R. R.
US December 6th, 2016
I'm glad that CMI has taken the time to debunk the conspiracy theorists (CTs) & pseudo-scientists without pulling any punches. It's misguided people like that who continually make it difficult for the better informed & scientifically literate Christians to be taken seriously. It's interesting, if not extremely embarrassing, to see people who believe in such flat-earth nonsense, to the point where they ignore directly observable data/evidence, & the difference between claims about history/origins & operational/repeatable science in the present. In another logic-defying stunt, they trust CMI & their more scientifically literate/informed family when they talk about creation/evolution, yet turn around & claim that CMI is pseudo-science when they show what ought to be self-evident to anyone with a shred of logical and critical thinking. It's very inconsistent, to put it politely. The CT crowd thinks that a government that so miserably failed to cover up the truth about Benghazi (e.g. including the Hillary Clinton email scandal), which involved very few people, can somehow "succeed" in getting tens of thousands of people across the globe to "cover up" the flat-earth "fact"? Are they "barking mad"? ;) CMI, keep doing what you're doing, & never pull punches. If they're so unwilling to be persuaded by directly-observable and reproducible data/analysis & so willing to accept obvious pseudo-science and CT stuff, then the case is probably not much different than trying to persuade an evolutionist that creation is a better explanatory framework for the real world. At the very least it should be made clear that we do NOT stand with them in asserting flat-earth & CT nonsense.

@CT crowd: CMI is doing you a service w/ facts & truth. You listened to them before. Listen to them now!
Phil K.
US December 6th, 2016
Wouldn't the first sailor be the first to determine that the earth wasn't flat? Seems to me that once you venture far enough out on a flat ocean surface, that you could look back over your shoulder and watch the land descend below the horizon, only to watch it ascend upon return. And I would think the ISS astronauts are the latest to figure out that the world is not flat. Maybe the moon is flat?
Richard P.
CA December 6th, 2016
Fascinating and very creative piece of work!
Robert R.
AU December 6th, 2016
I think Creation.com has talked about these Flat Earth believers at least twice this year. Why give so much time to them. Once I heard that the president of that society was an atheist anyway [by Creation.com or a book sold by them] I just figured if it isn't by some Biblical believer who was misled by ancient Geek philosophers, then why even talk about it. Evolutionists believe so much false stuff that when one believes the Earth is flat just ignore them. A simple google search came up with 'Daniel the president of the Flat Earth Society is an evolutionist... He says that his society now has 60 members.' It's a waste of time even dealing with crazy people.
Robert Carter
December 6th, 2016
It was only recently that our speakers began to report interactions with flat-earth believers across the world. Other creation ministries have had similar experiences. It is like a brush fire that springs up in multiple places at once, and one must get a jump on a brush fire before it gets out of control. True, we are spending a lot of time on a minor phenomenon, but we have multiple reasons for doing so. First, we want our speakers and supporters to have the best arguments when interacting with these people. Second, we want posterity to know that we are not in this camp (our opponents always try to tar us with as wide a brush as possible). Third, we do not want anyone else to fall into this trap. I cannot imagine there will be any more anti-flat-earth articles on creation.com, but this last one seemed appropriate.
Janco J.
ZA December 6th, 2016
Thank you Dr Carter for this well written article. It has become astonishingly frequent that one would encounter flat earth believers and I would dare to say that each one of us probably knows even at least one such person personally. I have recently become quite interested in amateur astronomy and one can only be humbled day in and day out with the beauty of God's creation. Another point that I have noticed that FET cannot explain is the existence of the South Celestial Pole (SCP), a point in the sky, found in the Southern Hemisphere, where by all other objects appear to rotate around as the earth rotates. Their model can explain the existance of the NCP, but according to my understanding true south, seems to be facing in different directions for various longitudes... The problem lies herein for FET : the SCP is the same point in the sky for everyone in the southern hemisphere, from South Africa to New Zealand. Basically, in Astronomy, there would be no way for an equatorial mount perform its function i.e. tracking objects along the Right Ascension Axis, if the earth was a disc. If this is something that one cannot grasp... one's objections to a Global Earth does, respectfully, not even deserve a response. Since some commentators (in the southern hemisphere) seem to want to be able to observe that the earth is a globe by walking outside to their backyard, I would advise you to buy a telescope with an Equatorial Mount and start doing some actual observational science. I would also advise some FET members to refrain from talking about science if you clearly have no interest in science.
Johan S.
ZA December 6th, 2016
Furthermore, unless your international flight is along the same longitude, you always end up in a different time zone. Tim, you might be familiar with the following example. About a month ago the mighty All Black Rugby team's winning streak of 18 unbeaten matches were ended by Ireland. The game was however played in Chicago of all places. Kick off was at 15:00 on 5 November local time and broadcast live all over the globe. Back in Ireland they watched the live game at 20:00, and here in South Africa we had to stay up till 22:00 for kick off. Meanwhile in New Zealand you saw the live game at 9:00 on 6 November! How do you explain this time zone variation for a single event? Judging by live tweets, spectators from across the globe saw it at the same time, in different time zones.
Robert Carter
December 7th, 2016
They claim that they can explain time zones, so your argument is not as good as it could be.

After consulting with Jonathan Sarfati, we came up with this:

The time zone argument is certainly conclusive against the old flat earth model. Medieval scholars like John Sacrobosco used it to good effect, and it’s much more powerful now (see A flat earth, and other nonsense: Time zones).

But since they claim to explain time zones, one should combine the time zone argument with something else, like the south celestial pole argument (see nearby comment) to make a solid proof.

But note that the modern flat-earth model claims to explain (away!) time zones by postulating that the sun really circles over the proposed disk of the earth. This is so absurdly contrary to what you can see every dawn and dusk: the sun, rises and sets piecemeal below the horizon, and without changing its diameter—it doesn't look like an expanding and shrinking circle as it would if were circling towards and away from us. Also note that the flat-earth model has to avoid even a pretense of being biblically based, because the Bible talks about the sun rising and setting (e.g. Psalm 113:3). As phenomenological or reference-frame language, this is compatible with the global geokinetic view, but certainly not with a sun perpetually overhead.

There one final, and huge, problem with the "spotlight" sun model of the Flat Earth Society: the spotlight would have to light up the earth in a wedge-shaped manner. A round spotlight would not flood everything along the same line of longitude at the same time. Central Africa would be lit before northern or southern Africa as that circular spot of light moved across the earth's surface.

In reality the time zone argument does not work for them, but you have to use the argument correctly.
Hans T.
NO December 6th, 2016
Now you know how extremely frustating it can be when someone presents pseudoscience as essential for being a Christian. At least the flat earthers don't have any significant financial backing.
Robert Carter
December 6th, 2016
Are you having a dig at us? Just in case, anyone reading our material should know that we directly teach that a belief in creation is NOT required for salvation.

See

Do I have to believe in a literal creation to be a Christian

and

Can Christians believe evolution

It would be good for you to know what you are arguing against.

And as far as funding is concerned, you cannot call our budget 'significant'. This is even more clear when you consider the enormous funding that our opponents receive. We do a lot with a little, however, so we feel that the donations we receive are not wasted.
Chandrasekaran M.
AU December 6th, 2016
Right from 16th century, people have done global circumnavigations using ships, planes and hot air balloons and even a circumnavigation via north and south poles. So, what is this flat earth propaganda about? The Bible does not teach about flat earth and other world views also do teach about flat earth!! Is there something common with a) molecules to moral homo-sapiens via mutations and selections, b) wholly man made global or flat earth warming even though the climate has been warming since the time when the ice age peaked and c) flat earth propaganda?
Robert Carter
December 6th, 2016
Since they claim you can travel across the world in a circle, circumnavigation is not a good argument...until one realizes that the methods they used to circumnavigate the earth depended on the earth being a sphere.

Some ancient worldviews did teach the earth was flat with a solid dome over it. Since the Bible is ancient, it should not be compared to modern worldviews in this regards. At worst, the biblical language is equivocal, meaning it does not expressly teach one way or the other. One can take certain passages out of context and attempt to support a flat earth, but then one must ignore other passages that contradict the idea. Yet, the spherical-earth passages seem to trump the flat-earth passages, by which I mean if you take Set A as true, Set B cannot be true (contradiction), but if you take Set B as true, Set A can be true (nested meaning).

I would not put your list of examples in that order, but yes, conspiracy theory is absolutely influencing this trend. The problem here is that they go too far and end up rejecting the Bible, 2,000 years of Christian scholarship, and simple observational science. In the end, their world is a world of magic and deception, which is very much unlike the way the Bible describes God's creation.
Egil W.
NO December 6th, 2016
I am a bit surprised really that so many holds a flat-earth-view(at all)thinking they have support from the Bible. I mean, to get a biblical worldview, you need to read up on all the verses and chapters who speak on any topic of research, and take all into account to give the best sense when these verses are first properly understood in their immediate context. Example: «And the waters prevailed so mightily on the earth that all the high mountains under the whole heaven were covered. The waters prevailed above the mountains, covering them fifteen cubits deep. And all flesh died that moved on the earth, birds, livestock, beasts, all swarming creatures that swarm on the earth, and all mankind. Everything on the dry land in whose nostrils was the breath of life died. He blotted out every living thing that was on the face of the ground, man and animals and creeping things and birds of the heavens. They were blotted out from the earth. Only Noah was left, and those who were with him in the ark. And the waters prevailed on the earth 150 days.» ‭‭Genesis‬ ‭7:19-24‬. ‭First we see: "...that all the high mountains under the whole heaven were covered. The waters prevailed above the mountains, covering them fifteen cubits deep." Then we notice: "...Only Noah was left, and those who were with him in the ark. And the waters prevailed on the earth 150 days." So, a flat earth would not really be a place where worldwide-covering water could stand fifteen cubits over the mountains... and prevail for 150 days. It would run off from over these alleged edges of this flat earth (a circular antarctica...), immediatly to drop beneath the level of the smallest of these alleged) mountains. Or more likely, never be able to cover the earth in the first place. = No parsimony with flat-earth.
Tim H.
NZ December 5th, 2016
Very good effort. But please explain why the Earth shows no curvature. I have argued against evolution for years and used the science of information to expose its ridiculous foundations, (life out of non-life replete with all the information that requires), and all the arguments using fossils and embryos etc. are rendered pointless because the evolution airplane cannot even get out of the hangar. You can throw all the maths you like at me to support your globe belief, but nobody seems willing or able to shine their light on the fundamental, personal and non-theoretical observations of large land masses seen from a great distance which I and thousands of others are seeing once our eyes are opened. If you cannot show curvature on the ground then you are just like the brainwashed life from non-life believers who accept that ridiculous notion as fact and then build their whole world-view upon this 'sand'. Christians have over time relegated the Devil to a minor or even non-existent role in human endeavours. The reality is the exact opposite and no field of human endeavour has been left untainted by Satan, including science and the Church. If the Earth is flat then it is a deception so huge in scale that its architects will have thought of most everything to defend it, including the use of 'useful idiots' in all fields of human activity. God is great whatever the Earth's shape or structure, this is not a salvation issue, but I do believe its consideration helps to bring into sharper focus the true breadth and depth of satan's plotting to usurp Christ. Genesis 3 is a bible text well quoted by creationists and it would be wise to always have it in mind when viewing the world we live 'in' but are not meant to be a part 'of'. Thank you, Tim
Robert Carter
December 5th, 2016
Explain why the earth shows no curvature? Open your eyes! You said "no", as if there is an emphatic lack of evidence. But this is demonstrably not true. And after you said "no" all I need to do is bring up a single bit of evidence for a spherical earth to prove you wrong. And I did so in this article! Read the main article linked at the beginning of this article for more evidence. It does not even appear flat on a local scale (ask any surveyor, GIS specialist, or military sniper and they will tell you how the curvature affects their work).

You say you and many others have seen distant landmasses? Yes, but there is a limit to the distance you can see and you can only see them under specific circumstances. The entire phenomenon (mirage) is explained by the diffraction of light by air of different temperatures/densities. This is simple, laboratory science. So, since both your side and our side expects to see this, it is a non-experiment. Thus you cannot use it to support your side! Worse, I believe there are certain aspects of that phenomenon that contradict your model, but there is no room to explain that here.

You say the Devil influences science? I can accept that so far as he influences people. But the Devil did not create this world. He did not create science. He did not create you. And he did not give you your ability to reason, to observe, or to draw conclusions. He is not in control. Thus, we are at liberty to use our God-given faculties for reason to draw conclusions about the world we live in. And when we do so, the earth is clearly a sphere. To say otherwise is to deny reality. Come away, my friend.
L. M.
CA December 5th, 2016
Thank you Dr. Carter for this thorough analysis! (Also, what a cool homeschool project for your children!)

It is so sad to see so many fellow-believers following after this flat-earth nonsense. Friends, do not give the atheists a legitimate reason to mock believers!

Comments are automatically closed 14 days after publication.