Dystopian science

Part 3: Rebuilding science from the ground up

by Robert Carter, Lita Sanders

In Part 1 and Part 2 of Dystopian Science, we set up a scenario where we are trying to rebuild science from the ground up. Humanity is recovering from a global catastrophe and almost all prior knowledge has been lost. But we have the Bible and can use it for guidance. This book gives us reasons for making two grand assumptions that drove the scientific revolution: 1) despite the fallibility of our senses, we can generally perceive the universe correctly, because God has created it in a way that conforms with His own internally consistent nature, and 2) we can properly interpret the universe with our God-given brains and our five senses. See Part 1 for more. But we also discussed how to struggle against false claims and false authorities in Part 2. If you have not read these, please go back and do so (particularly before commenting on this article!).

With these two assumptions and an ability to do simple experiments, you can figure out basic science from the ground up, because the propositions of operational science are true, self-supporting, and biblical.

God is a God of order (c.f. 1 Corinthians 14:33), and we can easily see this in Scripture. For example, He made the sun, moon, and stars “for signs and for seasons, and for days and years” (Genesis 1:14)—that assumes knowledge of astronomy, physics, mathematics, a concept of linear time, a calendar system, rationality, and the ability to make empirical observations—all in one verse! Thoughts like this help us to understand that there is a normative order in nature and provides the basis for a pragmatic, practical use of science.

Our thought experiment has turned out unexpectedly optimistic! God has given us all the foundation we need in Scripture to do science and to test the claims of others who claim to be authorities. So where do we start?

Step 1: Logic and math

First, we need to be able to think consistently. Logic is systematized, consistent thought. And we have the basis for that in Scripture, as we explained in part 1 of this series.

Next, we need to be able to do math. In one sense, math is just logic with numbers, but it is actually more fundamental and more important than that. There is a lot of assumption in math also. How do we justify those assumptions? Well, if we start with the Bible and treat it as an authority on every matter it covers, as it claims to be, we will also find math. There is addition (e.g. Genesis 5:3–5), subtraction (e.g. 1 Kings 6:37–38), multiplication (e.g. Matthew 17:24–27), division (e.g. Judges 7:16, 19), and fractions (e.g. Leviticus 27:27–32) in the Bible. We can even derive the associative, distributive, and communicative rules of addition and multiplication and a rough approximation for the value of pi (1 Kings 7:23–26) from its pages.¹ In fact, the Bible uses many of the most fundamental principles of mathematics. These statements in the Bible assume that mathematics is trustworthy and a means of obtaining truth, so that a person who starts with the Scripture has justification for their use of mathematics.

Clearly, we need to build some additional math tools beyond the bare-bones basic ideas. You can’t have a scientific discussion if you do not know how to count, but you also need that ‘ghastly’ subject of trigonometry. But if the ancient Greeks could figure out trig, so can we. In fact, the basic precepts of math are so simple that one does not even need a calculator to discover them. The point, the line, and the plane can be described in simple terms. 1 + 1 = 2 is always true. Once we establish the easy stuff, we will be well along our way. In fact, once the easy stuff is laid down, the more complex math will follow along naturally by deduction. But we don’t even need the hard stuff to jump-start science.

Step 2: Repeat experiments

Before we get into rebuilding science, we must be able to do repeatable experiments. This might take some time, because we might need to build a few different types of scientific instruments. We cannot, for example, discover that water always boils at 100° C until we invent a thermometer and decide upon a standard calibration (i.e. that 0 and 100 are the freezing and boiling points of pure water, respectively). But we can demonstrate, as many times as we like, that dropped objects always fall straight toward the earth (as long as there is no wind). The repeatability of experiments is something that absolutely must be established before science can advance. But again, we trust the world and we trust our perception of the world because we trust the One who created both the world and our senses.

Step 3: Build science

We are now, finally, ready to start rebuilding science. We have laid down a rationale, a method, and a philosophy. All of these work together and each of these has a biblical foundation. What we need to learn next can happen in any order. In fact, the following fields historically developed in parallel, often working off each other.

Physics

With some thought, we can show that objects consistently follow a curved path when they are thrown, that objects accelerate as they fall, and that heavy and light objects fall at the same rate. This is incredibly important work, for it will help us to establish the theory of gravity. By the way, these experiments were performed by Galileo (1564–1642) and helped pave the way for Newton’s (1642–1727) theory of gravity (published in 1687). Newton also gave us the laws of motion, and he co-invented calculus. We cannot build skyscrapers, launch rockets, or drive a car without a good understanding of physics.

Geography

The discovery of the size of the earth (just about all ancient cultures already believed it was a sphere) did not occur until someone had a very good estimate of the distance between two distant places. This happened in ancient Egypt. The head of the Library of Alexandria at the time, Eratosthenes (276–194 BC), knew the distance between Alexandria and Aswan (about 5,000 ‘stades’), and he knew of a report that the sun lit up the bottom of a well in Aswan at the summer solstice. In other words, it was straight up, 90 degrees, on that one day. This was not the case where he lived in Alexandria. So he measured the angle of a shadow cast on the solstice in Alexandria: one fiftieth of a circle (~7 degrees from the vertical). He then knew that he was 1/50^th of the way around the earth from Aswan. Since he knew the distance quite well, multiplying it by 50 gave him an estimate of the circumference of the earth. Depending on which ‘stade’ you use, he may have been within 1% of the real value of 40,075 km (pole-to-pole). By the way, Eratosthenes coined the term geography. We reject him at the cost of rejecting over 2,200 years of non-conflicting scholarship.

Think about it: you can figure out the size of the earth with a plumb bob and a stick. This is not astrophysics! Our society should quickly re-discover how large planet Earth is.

There are some that say Eratosthenes’ experiment would also work on a flat earth. That is true, if the earth were flat, but it also allows us to test the flatness of the earth directly. We know the earth is not flat, because if you repeated the experiment at different latitudes you would get different results for the height of the sun. The angle of the sun always equals the latitude, that is, the distance around the globe from the place where the sun is vertical. At certain times of the year near the North or South Pole, the sun traces the horizon. It has zero height for the observer. If you were to apply Eratosthenes’ experimental setup to your location on those days, either 1) you are on a global earth and are 90 degrees around the earth from the line where the sun is straight overhead, or 2) you are on a flat earth and the sun is rolling along the ground, which, of course, cannot be true.

This is an example of the idiocentric model we described earlier. It is also an example of non-discriminating information. One cannot conclude the earth is round or flat from Eratosthenes’ single measurement. But if you were to take the same measurement at different distances north or south (either on different years or on the same day after asking a trusted friend to help you with the experiment), the results can only be interpreted in terms of a spherical earth.

Astronomy

Credit: Andonee, Wikipedia

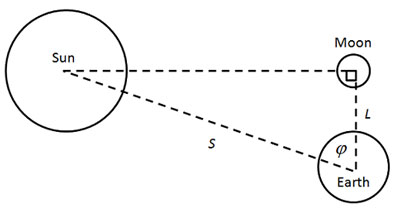
Following on the heels of geography, astronomy is one area of science in which we can make huge strides with little effort. We can know that the earth is a sphere by observing the shadow cast on the moon during lunar eclipses. We can also know that the sun is much further away than the moon by observing the width of the earth’s shadow during one of those eclipses. In fact, this is what Aristarchus of Samos (310–230 BC) did, several centuries before Christ. His measurement was crude (because it depended on knowing exactly when the earth, moon, and sun formed a perfect right triangle), but his reasoning was sound. It took many centuries to determine the exact distance to the sun, but this was helped greatly by Captain James Cook, who was able to record the transit of Venus across the face of the sun from Tahiti in 1769. Simultaneous measurements from England allowed the triangulation of the sun’s distance, using nothing more than a few primitive instruments and the math you learned in your first or second year of high school.

Solar system astronomy is not rocket science. Anyone can do it. In fact, James Bradley figured out the speed of light (to a high degree of accuracy) by simply looking at two stars every night in a telescope that was strapped to his chimney so that it could not move. He could, however, tilt the eyepiece a little and he took careful notes on the position of the eyepiece through the seasons. He did this for 20 years and published his result in 1729. Did you get that? We knew the speed of light nearly 300 years ago and this was done with extremely simple tools. The tilting changed over time, and he reasoned that this was due to the earth moving with respect to the stars. We can explain it in this way: If someone threw you a ball and you were trying to catch it in a pipe in such a way that it did not hit the walls of the pipe, you would have to angle the pipe toward the direction of the throw. In the same way, a telescope must be angled ever so slightly in order for the light coming from a star to not hit the side of the telescope, because as the earth revolves around the sun it is sometimes moving toward the star and sometimes moving away from the star. But the angle also depends on how far away the star is from the North or South Celestial Pole.

commons.wikimedia.org

And Friedrich Bessel made the first measurements of stellar parallax (the little wiggle close-in stars make as the earth goes about the sun each year) in 1838. He determined that the star 61 Cygni is only about 10 light years away. The ‘wiggle’ was less than 0.00009 degrees! But he was able to measure this with good critical thinking and a telescope that is comparable to something you can order out of a catalogue today.

commons.wikipedia.org

Chemistry

Do you want a smart phone in our future earth? Then you are going to need to know a lot of chemistry. The phone in your pocket requires something like 75 different elements to manufacture, including exotic elements like dysprosium and terbium, let alone the more well-known ones like carbon, copper, and silicon. Each of these is going to take a lot of experimenting to discover and then to figure out what they are good for.

But we are also going to need to know how to make glass (for our thermometers), metal tubes (for our telescopes and microscopes), and we need to learn that mercury, lead, and arsenic are poisonous, even if they can be used for several different medicines (that are no longer considered safe). This requires chemistry. Dmitri Mendeleev (1834–1907) required enough elements to be discovered (65 of the 118 now known) for him to figure out a few trends. The result was the periodic table (first published in 1869), a triumph of experimentalism and a great driver of hypothesis testing. For example, empty places in his table led directly to the discovery of multiple elements, like germanium, which is below silicon and above tin in the table.

We might have some false starts. In fact, chemistry was held back for many years until the pioneering work of Robert Boyle (1627–1691) helped build a foundation that Antoine-Laurent Lavoisier (1743–1794) later used to overturn phlogiston theory. But the exploration of chemistry is a must if we are to restart civilization.

Yet chemistry tells us little about the nature of reality. We will learn little about the shape of the earth or its relation to the heavenly bodies from chemistry alone. We just need it to build some important tools.

Biology

The subject of biology was a late-comer in the world of modern science, even though there are a lot of biological ideas we can glean from Scripture. For instance, Genesis 1 tells us that animals reproduce “after their kind”. But we also know that animals can speciate, and sometimes very quickly (Genesis 47:17 speaks of horses and donkeys as distinct creatures about 600 years after the global flood). We know that some animals can be tamed (James 3:7), but others like Behemoth and Leviathan cannot (Job 40–41). We even know where babies come from (Genesis 4:1).

However, while ancient people clearly knew a lot about practical things, and they had surprisingly sophisticated knowledge when it came to raising livestock and growing crops, it took a long time to figure out what living things are made of, how they reproduce, and how they work. Disease theory is less than 200 years old, and genetics is even younger than that. The reason biology bloomed so late is that life is incredibly complex. In fact, we have only just begun to probe its mysteries. We trust that biology will be studied as we emerge from our dystopian scenario, and we trust that God will be praised with each new bit of understanding, as the psalmist said:

For you, O LORD, have made me glad by your work; at the works of your hands I sing for joy. (Psalm 92:4)

Detours from sound science

Will evolution and billions of years be re-invented? We saw earlier how biblical thought is required for science to be re-established. However, because there will always be those who want to deny God, it is likely that some will overextend the idea of methodological naturalism to deny creation, similar to what happened during the 18^th Century Enlightenment. Methodological naturalism applied to astronomy will lead to the idea that the universe is billions of years old, because some stars are much further away than 6,000 light years. And applied to biology, it will lead to the idea of evolution. This does not mean that these people will be correct, only that a rejection of God, once science is established on biblical principles, would naturally lead to such conclusions.

Likewise, there will always be some who argue for non-real alternative theories (like the modern ‘flat earth’ theorists). But a good dose of science from a biblical foundation should help us to avoid those pitfalls. There is no reason to dive head-first down the rabbit hole. The world is real, understandable, and physically non-contradictory. If we trust the Bible, we will be able to rebuild science. And when we do, we will be bringing glory to the Creator, the God of the Bible.

Conclusions:

Our dystopian scenario is not without hope. It is also not without science. If we take a biblical approach to the world, we will jump-start learning. In fact, we believe that science is inherently biblical and that a biblical approach to studying science will allow us to rebuild it, quickly, from scratch. In so doing, we will be following in the footsteps of the founders of modern science, who almost unanimously believed in the Scriptures and used it as a basis for their thinking.