First published:
Journal of Creation
20(3):95–103
December 2006

Browse this issue

Subscribe to Journal of Creation

Evidence for multiple ring growth per year in Bristlecone Pines

by Mark Matthews

Photo by John Woodmorappe

Figure 1. Bristlecone Pine growing in less than ideal conditions.

Growing in the White Mountains of eastern California are what are thought to be some of oldest living trees on Earth. The tree with the most rings, dubbed ’Methuselah’, is thought to be about 4,600 years old. One might expect then that the White Mountains host some of the best growing conditions on Earth. In fact, the opposite is true. Ironically, the alleged oldest trees grow in some of the worst imaginable conditions. Conditions are so bad that few other plants can survive: short cool summers with a growing season thought to be only several weeks long; desert-like aridity (250 mm of precipitation per year, mostly as snow); many trees grow out of little more than cracks in dolomitic rocks. Strong winds coupled with air that in the summer is said to be the driest on earth,¹ and the rocky ‘soil’ (where there is any ’soil’), means that what little rain does fall will evaporate or drain away quickly (figure 1). It may be that these exceptionally harsh growing conditions are the key to understanding why some of these Bristlecone Pines have so many rings that they appear to live about ten times longer than BCPs which are growing in comparatively good conditions!

The thesis of this paper is that, under conditions where water is scarce, BCPs grow multiple thin rings per year rather than one thick ring (as has been documented in other species of gymnosperms and angiosperms² ). Further, I hypothesize that the multiplicity growth habit and the strip-growth habit conserve a tree’s resources, especially water.

Multiplicity is common under the right conditions

Perhaps the best evidence that some BCPs can grow multiple rings per year is the fact that it has already been demonstrated. Lammerts, a creationist, induced multiple ring growth in sapling BCPs by simply simulating a two week drought.³ Some dismiss this evidence, saying that while multiplicity has been demonstrated in young BCPs, it hasn’t been demonstrated in mature BCPs and therefore may not occur in mature BCPs.⁴ While this hypothesis could be true, surely the burden of proof should be on those who propose that what happens in immature trees doesn’t happen in mature trees.

An expert in the genus Pinus didn’t seem to have any problem believing that White Mountain BCPs grew multiple rings per year. In his book, The Genus Pinus, Mirov states, ‘Apparently a semblance of annual rings is formed after every rather infrequent cloudburst.’⁵ If an expert like Mirov readily accepted multiplicity in these BCPs, then perhaps the doubters of this notion should at least give the evidence a serious examination.

It is important to understand that the idea that mature trees can grow more than one ring per year is not a highly speculative hypothesis. It is well established that mature trees of many species of both angiosperms and gymnosperms, including other species of the genus Pinus, can grow multiple rings per year, especially under the types of conditions in which some of the BCPs in the White Mountains grow. Glock et al. published a large study in 1960 documenting the common occurrence of multiple ring growth per year, under conditions similar to those in the White Mountains.² They found that multiplicity was more than twice as common as annularity, and conclude that probably very few annual increments, over the entire tree, consist of only one growth layer⁶ (that is, only one ring).

In addition to solid direct evidence that these BCPs may be capable of growing multiple rings per year, there is abundant indirect evidence of multiplicity.

Indirect evidence of multiplicity

To build a master-chronology of BCPs believed to extend back over 8,700 years,⁷ researchers must use wood from dead trees to extend the chronology beyond the lifetime of currently living trees. The older parts of the chronology come from dead wood found lying on the ground near the living trees. This means that some pieces of wood in the earliest part of the chronology would have had to lie around on the ground for more than 7,000 years!⁸ Immediately, one wonders how wood can lay on the ground for 7,000 years without rotting, eroding away or otherwise disintegrating. Some have speculated that the cool, dry climate and high resin content of the wood preserve it against fungal rot, insect attack, and weathering. But this explanation doesn’t make sense given the disintegration that has occurred in the dead portions of living strip-growth trees.

Figure 2. Left picture (A) shows strip-growth; in this case spiral strip-growth (live bark is the darker strip spiraling up trunk). (B) depicts the cross-section of a tree that has been growing in a strip-growth habit for many years. Notice that the cross-section has become more rectangular than circular. (C) depicts the cross-section of a strip-growth tree where the wood not directly beneath the strip-growth has decayed away over time. How could this wood decay away in a fraction of the time that wood on the ground has lain un-decayed?

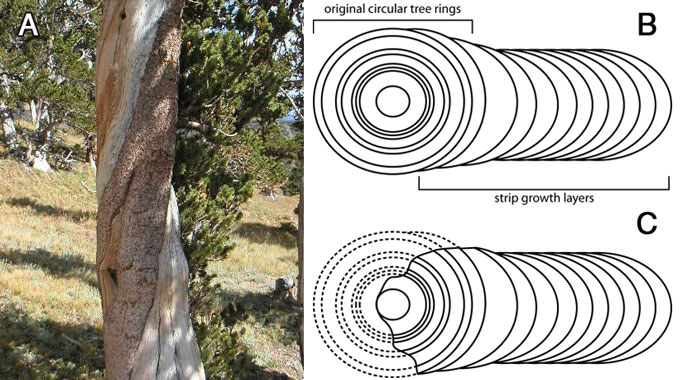
Strip-growth is a peculiar phenomenon found in all BCPs with more than about 1,500 rings. In strip-growth trees, most of the tree has died, but there remains one thin strip of living bark running up the side of the tree providing water and nutrients to the small portion of the tree’s crown which is still living. The added growth layers in strip-growth trees cause the tree to become slab shaped instead of cylindrical. Schulman says (speaking of the oldest of the White Mountain specimens found at the time), that in the strip-growth trees, the dead portion of the trees has been eroded down to the pith (centre), ‘… erosion of the barkless areas had been proceeding for one to two millennia and had reached to the pith or near it’.⁹ How can dead wood lay on the ground for up to 7,000 years while the dead wood in strip-growth trees completely disintegrates in a fraction of that time? Perhaps the wood on the ground isn’t nearly as old as thought (figure 2).

Figure 3. This photo shows John Woodmorappe holding a piece of downed BCP while a cross-section is being sawn for further study. This tree was sampled at a prior unknown date. The fingers of John’s left hand appear to be resting on the old sawn surface—probably where a previous cross-section was taken (although John couldn’t verify this). There are some obvious signs of decay on this old sawn surface that have occurred since the time it was freshly sawn. (Compare the surface that the fingers are resting on to the freshly cut surfaces). (After Woodmorappe,¹⁰ p. 126).

Also consider that in the climate of the White Mountains, these dead pieces of wood are subjected to many freeze/thaw cycles during the year which would tend to tear the wood apart through mechanical freeze/thaw processes. It seems strange, then, that researchers looking for old wood can’t get any clues about the age of a piece of dead wood just by looking at it.¹⁰ The pieces of wood which have been lying on the ground dead for supposedly thousands of years don’t typically show any more signs of ageing/decay than wood which has supposedly been laying there only several hundred years. In figure 3, dead BCP wood shows some obvious signs of decay. Why, then, do these ‘younger’ pieces of wood show just as much decay as pieces of wood which have been decaying for thousands of years? Shouldn’t the supposed decay inhibitors at work in the ‘old’ dead pieces be effective in the ‘younger’ pieces of dead wood?

One would also expect more dead wood lying on the ground from all those supposed past millennia if the wood is capable of surviving on the ground for thousands of years. Woodmorappe and others have found that dead wood dating to the earliest millennia is very rare.¹¹ If this ‘ancient’ dead wood is so resistant to decay processes that it looks as fresh as wood only a few hundred years old, then it would seem it should be about as abundant as wood from more recent millennia; or, at a minimum, that there should be an approximately linear relationship between the amount of wood remaining on the ground and the millennia in which it grew. In a limited study, Woodmorappe didn’t find such a linear relationship but more of a log-normal distribution of ages with the distribution skewed toward the younger ages.¹¹ On the other hand if these trees, living and dead, are all about the same maximum age, but some grew more rings per year than others, then Woodmorappe’s observations begin to make sense.

The claim that wood can lay on the ground undecayed for 7,000 years is even more fantastic when one considers the rate at which the mountains that these trees are growing on are eroding away. LaMarche¹² has found an erosion rate of about 1 foot (30 cm) per 1,000 years in the White Mountains in general, and a higher rate in the areas where the oldest trees grow. (The actual erosion rate may be much higher than LaMarche reports because he derived these erosion rates based on the tree-ring records of living trees assuming annularity of rings—an assumption that this paper contests). How is it possible that seven feet (213 cm) of dolomitic surface, can erode away over the course of 7,000 years, while dead wood could remain essentially in place on the surface of the ground over that same period? Can the dead wood really be that much more resistant to destruction than the rocks are?

We find more evidence for multiplicity of rings when comparing the growing environments of BCPs having thousands of rings with those having only a few hundred rings. The White Mountains afford the BCPs growing there numerous ‘micro-environments’ (that is conditions in the immediate vicinity of an individual tree). It is therefore baffling that the trees with thousands of rings grow only where water and soil are most scarce! After studying the environment of ‘old’ BCPs, LaMarche notes, ‘Comparative aridity thus seems to be an important characteristic of the “old-age habitat”’ and ‘Thus, high life expectancy is apparently related to the frequent occurrence of sub-optimum moisture conditions.’ Consequently, ‘There is a large concentration of ancient trees on arid sites at the lower forest border in the White Mountains.’¹³ Conversely, LaMarche found that where moisture conditions were better, as in valley areas where a decent soil can accumulate, none of the BCPs reach the ancient ‘ages’, ‘No old bristlecone pines are found in the valley bottom, which is a sheltered area with deep colluvial soil and gentle surface slope.’¹⁴ Strange—trees in decent growing conditions only live to several hundred years, similar to the maximum age of many other tree species, but trees growing nearby in a microenvironment with little water can live to several thousands of years. These observations would make more sense if both sets of trees actually live to about the same maximum ages, but the trees growing where water is scarce grow multiple thin rings per year rather than one thicker ring. One explanation is that such a growth habit conserves water.

Similarly, researchers have found that in the central area of a stand of BCP trees, where growing conditions are the best, the trees do not have more than several hundred rings. But at the margins of the stand, where the soil thins and growing conditions become progressively poorer, the trees with the most rings are found.¹⁵ It seems more probable that all the trees in the stand are about the same age, but that the trees growing at the margins are starved for water and grow multiple rings to conserve water. If there are no truly ancient BCPs—only BCPs which grow multiple rings per year—then Woodmorappe’s observation that ‘old BCP trees do not seem to show some typical biomarkers of ageing’ also makes sense.¹⁶

Figure 4. Typical tree cross-section, Ring B is the growth layer that grew over the layer represented by ring A.

Consistent with the above observations are the observations of Larson et al.¹⁷ In their study of US and western European trees that grow out of cliff faces, they found many ancient trees with exceptionally thin rings, and often exhibiting strip-growth. Again, it’s likely there isn’t much soil on a cliff face to provide for water storage between precipitation events, so the cliff trees may be using multiple ring growth per year to conserve water.

Can multiplicity conserve water?

If the basic proposition of this paper is correct—that there are no truly ancient BCPs, only BCPs which have grown multiple rings per year under xeric (dry) conditions—what is the connection between multiplicity and water scarcity? Could it be that multiplicity somehow conserves water, thereby allowing a tree to survive? To understand how multiplicity may help a tree conserve water, it is necessary to understand some tree anatomy.

Figure 5. The dark-wood is caused by the wood cells becoming gradually smaller. When growth begins again the first cells formed are large; this makes the outer edge of the dark-wood sharp and the inner edge diffuse. Wood growth is to the right in both frames. The ring widths are about 0.5 mm.

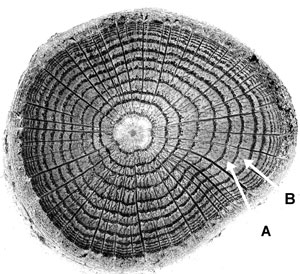
Tree growth can be conceptualized as a tree continually adding one layer of wood after another to itself, over its entire surface area. It is as if thick coats of paint are added over the surface of the whole tree one at a time. This method of growth causes the wood of the tree to have the distinctive pattern seen on a stump when a tree is cut down. The basic pattern that we see is of concentric circles like the cross-section in figure 4. Each ring in the figure represents the cross-section of one growth layer that grew over the surface of the whole tree but which we are now seeing only in cross-section. In figure 4, ring B is the growth layer that was added on top of the growth layer that grew right before it, represented by ring A. Not all trees exhibit this growth-ring habit, but most species in temperate zones of the world do. For trees that do exhibit growth rings, it is normal for them to grow one ring per year under normal growing conditions.

In BCPs each growth-layer or ’tree-ring’ (the terms are synonymous), consists of a light coloured band of wood coupled with a dark coloured band. The radial growth in a tree occurs due to a thin layer of cells just under the bark, called the cambium. As the cells in the cambium divide, they add wood to the outer surface of the tree just under the bark. The light coloured wood is often called the ‘early-wood’ because, under the assumption that each growth layer represents one year’s growth, the light coloured wood represents the growth that happens earlier on in the growing season. The dark coloured wood is called the ‘late-wood’ or ‘dense wood’. The cells that make up the late-wood are smaller, the cell walls are usually thicker, and there is a higher resin content in these cells. Since the cell walls appear dark and more of the late-wood consists of cell walls, the late-wood has a darker appearance and is more dense (figure 5). (Throughout the remainder of this paper I use the terms ‘light-wood’ and ‘dark-wood’ rather than the conventional ‘early-wood’ and ‘late-wood’, because these terms describe the wood rather than reinforce the idea that these kinds of wood only grow during certain times of the year—which is incorrect in some cases).

Figure 6. Trees with only one growth increment per year (top) have sap-filled wood in constant contact with the bark throughout the growing season. In trees growing multiple rings per year (bottom) the dark-wood layers may serve as barriers to radial movement of water during the growing season, thereby reducing water loss through the bark.

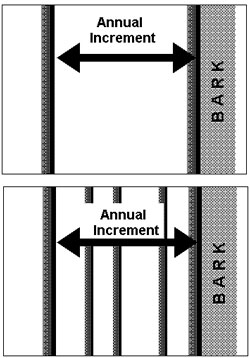
Trees lose water naturally from their leaves or needles during photosynthesis. Trees can also lose a significant amount of water vapour through the bark.^18–20 Any mechanisms that slow the rate of water loss out through the bark would be a great advantage to the trees in xeric conditions. Since the dark-wood has thicker cell walls, higher resin content, and smaller and fewer pits for conducting water, it is possible that the dark-wood retards the movement of water in the radial direction better than the thin-walled, low-resin, heavily pitted, light-wood cells. Perhaps this is why during the winter dormant season a tree has a layer of dark-wood right beneath the bark; it may be a design feature of the tree to help prevent water loss out of the bark during the winter dormant season. If this hypothesis is correct, and the dark-wood slows the radial movement of water and reduce the rate of water loss out of the bark, then a BCP having just one thicker layer of highly conducting light-wood in constant proximity to the bark throughout a growing season will loose more water through the bark than a tree which grows multiple thin rings, because each dark-wood layer would serve as a barrier to the radial movement of water (figure 6). A possible test of this hypothesis might involve measuring rates of water loss through the bark of thick-ringed BCPs and thin-ringed BCPs to see if the thin ringed BCPs lose less water than thick-ringed ones.

Conserving resources, mainly water, may also explain the mysterious strip-growth habit of the trees with thousands of rings. LaMarche notes that ‘Attainment of an age greater than about 1,500 years apparently depends on the adoption of a strip-growth habit.’²¹ This ‘strip growth’ habit is caused by the cambium dying around most of the circuit of the tree such that there is only one long living strip of bark running up the side of the trunk. The added growth layers cause the tree to become slab shaped instead of cylindrical. Strip growth allows the surface area of the bark to be minimized and resources to be conserved.

A tree growing in a normal manner (that is, adding growth layers around its whole circumference) requires that each centimetre of increase in trunk or branch radius adds about 6 cm of circumference, and a corresponding increase in surface area. added surface area increases water loss through the bark. It also means that as the tree gets older and bigger, an ever-increasing amount of wood has to be added for each ring of the same width. To keep up this rate of wood addition would require that the tree have basically unlimited access to resources needed to grow—including water. But under strip growth, the tree doesn’t use an ever increasing amount of resources to add each new growth layer; it takes about the same amount of resources each year to add each new growth layer (figure 7). Perhaps the switch to strip-growth takes place when the tree has reached a point that it can no longer add complete new growth layers because of resource limitations.

Figure 7. When a trunk or a branch is adding an increment of growth around its whole circumference (left), the addition of increment B takes more resources than the addition of the previous increment A of the same thickness. But under strip-growth (right) increment B takes about the same amount of resources to grow as the previous increment of the same thickness A.

Most of the water is conducted up the tree in the ‘sapwood’, which comprises the rings just underneath the bark; the ’heartwood’ does not conduct much water up the tree. When strip-growth occurs (as is the case with the White Mountain BCPs with thousands of rings), the strip of live bark and associated sapwood in the rings immediately beneath it only feed one or a few main branches; the rest of the tree dies because there are no more conducting tissues to feed it. The dead part of the tree begins to dry out and eventually decays. When the water conducting cells of the tree become dry (a condition known as cavitation) they serve as an effective barrier to water movement. Thus, the many rings consisting of cavitated cells would serve as a very efficient barrier to water loss from the relatively small portion of conducting sapwood beneath the live strip-bark. In this way very little water would be lost from the dead portion of the strip-growth tree.

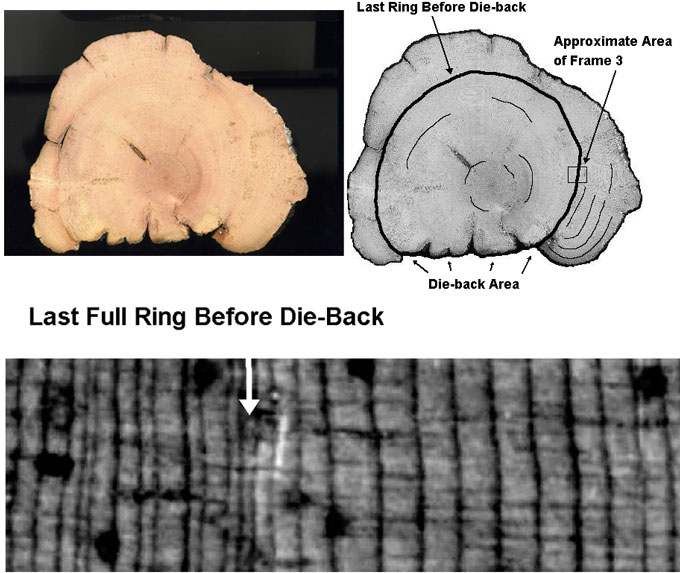
Support for the hypothesis that strip growth allows for better survival when resources are limited can be seen in the BCP cross-section of figure 8. The tree experienced cambial die-back over about a fourth of its circumference, after which it immediately started growing thicker rings than before the die-back occurred. Because the tree had less surface area to cover during its growth increment after die-back, a thicker increment could be grown even though the accessible resources remained the same.

Figure 8. This cross-section demonstrates that after die-back (when strip-growth begins) a tree has enough resources at its disposal to grow thicker rings than before die-back. The upper-left frame is a scan of the whole cross-section. The upper-right diagram shows where part of the circumference experienced die-back allowing more vigorous growth around the remaining live part of the circumference. The bottom frame shows the last 12 rings formed before die-back (left) and first 12 rings formed after die-back (right). Note that the average ring is much thicker after die-back occurred. The cross-section is about 24 cm at its widest point. The bottom frame is about 0.64 cm wide.

This leaves open the possibility that BCPs under certain conditions may switch between annual growth rings and multiple growth rings per year several times during its life. For example, when the tree is young and its circumference is small, it may have access to enough water to meet its basic needs, so it grows only one ring per year. As it ages and the surface area of the tree expands it loses more and more water out of the bark, but by switching to a multiplicity growth habit it can conserve water. As the tree continues to expand in surface area a point is reached where the tree can no longer sustain growth over its whole surface area. By switching to strip growth it reduces drastically the surface area of tree which is a pathway for water loss. Growing in a strip-growth habit, the tree may now have access to enough water that it can maintain its growth using only a single ring each year. If for some reason the water supply is no longer sufficient, the tree can begin growing multiple thin rings per year again.

Rebuttal to claimed evidence for annularity

The initial reason that scientists studying BCPs in the White Mountains thought that they were growing only one ring per year is because they believed it was fairly easy to tell when a tree was growing more than one ring per year. As seen in figure 5, the beginning of the dark-wood is usually a zone that is somewhat fuzzy; that is, the light-wood grades gradually into the dark-wood. This is because the light-wood cells gradually becoming smaller as new cells are added. However the dark-wood band usually ends abruptly, producing a distinct line which marks the outer edge of the dark-wood. This results from the cells of the dark-wood typically getting smaller and smaller until they stop and are followed by distinctly larger cells making up the light-wood of the next ring. So, the inner edge of the dark-wood is usually gradual, fuzzy and indistinct; but the outer edge of the dark-wood is usually abrupt and distinct. This was interpreted as meaning that late in the growing season of each year, a tree would slow down its growth until it gradually came to a complete stop (this stop corresponded with the last latewood cells that were added to the circumference of the tree). No further growth would take place until the beginning of the next growing season; at that time the tree began vigorous growth again and the cells which began to grow were the large early-wood kind.

Sometimes dark-wood is produced which does not have a distinct outer boundary, but a fuzzy one, like the inner boundary. Under the microscope it can be seen that the cells of dark-wood do not end abruptly but gradually start getting bigger again. This is usually interpreted as the tree, for some reason, slowing down its growth during the growing season, but then picking up its growth again before beginning the final slow down that occurs at the end of a season. The entire growth band for that year would then include a ‘false’ band of dark-wood (such dark bands are designated as ‘false’ because they did not occur at the end of the growing season as ‘true’ dark bands should). If not detected, false bands would lead one to believe that two rings were present, representing two years, rather than one year’s worth of growth with a ‘false’ dark band in the midst of that year’s light-wood. So it was assumed that ‘false’ rings (and thereby multiplicity) could be easily detected because the outer edge of the dark-wood would be less distinct than the outer edge of normal annual rings.

Later, however, Glock et al. demonstrated that in dry climates, not only are ‘false’ rings common in many species, but the bands of ‘false’ dark-wood can have outer boundaries that are every bit as distinct as the outer boundaries of a true annual ring.² Therefore, ‘false rings’ can be indistinguishable from ‘true’ annual rings; ‘ … the growth layers resulting from intra-annual flushes [of growth] may, and commonly do, possess outer borders indistinguishable from the borders terminating the annual increment … .’²² So we see that ‘false’ dark-wood does not always have a fuzzy outer boundary.

Figure 9. Photo of thin-ring dark-wood with diffuse inner and outer boundary. It is difficult to tell which is the inner, and which is the outer boundary. The frame is about 0.1 mm wide.

LaMarche and Harlan see four lines of evidence as supporting the annularity of rings in BCPs.⁴ The first is that the dark-wood bands in BCPs do not have diffuse outer boundaries, implying that none of the rings are ‘false rings’. Glock et al. showed that at least some species can have ‘false rings’ that are indistinguishable from the annual rings.²² It may well be that White Mountain BCPs have false rings which are indistinguishable from annual rings. It is also often the case that extremely thin rings have inner and outer boundaries which are virtually identical (figure 9). Additionally, Glock et al. found that about 99% of the extremely thin rings and partial rings were ‘false’ rings.²³ White Mountain BCPs with thousands of rings abound in thin and partial rings.^24,25 In fact, some ring sequences consist of rings so thin (averaging 0.1 to 0.2 mm and less²⁶) that a microscope is needed to distinguish one ring from another. Some ring bands are the thinnest possible, being only one cell thick!²⁷ (Figure 10 shows a thin ring with a light band only two to three cells thick.) Finally, further evidence of ‘false’ rings can be seen in figure 11 which shows three distinct BCP dark-wood bands that are all connected together, strongly indicating that they were all formed during the same growing season.

Figure 10. Photo of a ring where the light-wood is only 2 or 3 cells thick. The frame is about 0.2 mm wide.

The second line of evidence comes from a 3-year study by Fritts where continual growth measurements were taken on a few Bristlecone Pines in the White Mountains of California.²⁴ However, these measurements were taken from trees in a valley-like area where the soil was substantial enough that soil moisture measurements could be taken (the ‘soil’ is too rocky in most of the ‘old’ tree areas to allow moisture level measurements), and all these trees were deemed ‘young’. As discussed above, BCPs in decent soil may not grow multiple rings per year, as a general rule, because they have access to enough moisture in the soil. Also, the trees are deemed to be ‘young’ because they don’t have thousands of rings, which, according to my hypothesis in this paper, means they are probably not growing multiple rings per year.

With respect to the third line of evidence, LaMarche and Harlan claim that samples obtained in 1971 cross-match with White Mountain Bristlecone Pines sampled in 1954 by Schulman.⁹ They found that most trees have formed exactly 18 rings in the period 1954–1971²⁸ (a few formed only 17 rings, none formed more than 18 rings) indicating that the BCPs did not grow more than one ring per year. The argument hinges on a claimed cross-match that can’t be verified and could be incorrect given the inherent subjectivity of cross-matching. Beyond that, it appears that none of the living trees sampled in 1971 were ‘ancient’ ones (i.e. with thousands of rings), so it is possible that the trees in this study were growing only one ring per year.

The fourth line of evidence has to do with frost markers found in a number of trees in the 87^th ring before the ring representing 1971. If each ring represented a year, then this frost would have occurred during the growing season of 1884. After finding these frost markers, LaMarche and Harlan went back through weather records and try to make the case, based on sketchy weather data, that there could have been a frost around 9–10 September 1884 which caused the frost damage in the trees rings.

Figure 11. Three dark-wood bands tied together. B continues to the right of A with the black vertical line at approximately the same location. If traced to the left, the dark-wood band in A indicated by the white arrow merges completely with the dark-wood band above it. Likewise, the same dark-wood band in B (again indicated by the white arrow) if followed to the right blends in completely with the dark-wood band below it, giving the strong indication that all three dark-bands were grown during the same growing season. The total length of A and B together is about 2 cm.

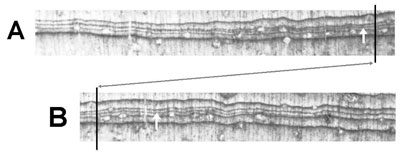
The argument is unconvincing for a number of reasons. Fritts²⁵ found that Bristlecone Pine in the White Mountains stopped growing in late July to early August. The trees would still have to be growing when the freeze supposedly occurred ⅓ of the way through September (LaMarche and Harlan don’t actually mention where in the growth ring the damage occurs, but even if it were in the very last formed part of the ring, 9 September seems like an unlikely date for the trees to still be growing). In addition, it goes against the general rule that frost damage usually occurs early in the growing season due to a late frost.²⁹ LaMarche and Harlan claim that the 87^th ring was the first ring with frost damage encountered when counting back from 1971. This means there shouldn’t have been any other unseasonably cold spells between 1884 and 1971 that could have caused frost damage, but LaMarche and Harlan don’t address this question. The frost could have occurred much more recently if the trees have grown extra rings per year. Lastly, there apparently isn’t good weather data available for the White Mountains back in 1884. LaMarche and Harlan end up having to rely on weather data that is vague and over 400 miles away for making a weak case that there could have been a frost around September 9, 1884.

Another idea encountered in the literature is that the cross-datability of BCPs somehow negates the possibility that the rings involved aren’t annual. I have never seen the logic behind this contention explicitly stated, but perhaps the thinking is that if trees were putting on extra rings per year more or less randomly, then we shouldn’t be able to match the patterns between two trees because one tree might have grown one ring in a year and another tree might have grown two or more. However, if the timing of the growth layers is triggered by environmental factors (like rain events), it could very well be that all trees growing in a similar environment behave similarly. So, for instance, if there were two large precipitation events and one smaller one in a particular year, then it might be expected that all the trees growing near each other in similar growing conditions would grow two larger rings and one thin ring that year. In this way the ring-width sequences would be similar, but not every ring would represent an annual increment. Glock et al. concur that cross-dating doesn’t prove annularity, ‘The fact that the thin, entire growth layers or lenses match from one tree to another does not prove their annual character.’³⁰

Suggestions for demonstrating multiplicity

The following are some ways that additional direct evidence for BCPs growing multiple growth layers per year can be obtained (remembering that trees growing in water scarce conditions are the ones most likely to grow multiple rings a year):

1. Find old photos (from perhaps a private land owner, nature photographer, the National Park Service or the US Forest Service) of individual Bristlecone Pine trees or stands of trees, where the date (or year) that the photograph was taken is known, and the location of trees is known. Go to where the original photo was taken and try to find new trees or new branches that have grown since then. Get permission to core the tree or branch (or better yet see if the whole tree or branch can be cut, special permission may be needed on public land). The age of the photo will provide the maximum age that the branch or tree can actually be—see if the number of growth-rings exceeds this maximum age. A slight variation of this method would be to find a private individual or public servant who knows (and can preferably document) exactly when a certain Bristlecone Pine tree was planted or a certain road was built or land cleared.
2. Place time tags in the trees by freezing with dry ice to produce ‘frost’ damage or by watering with a dye that is transferred to the sap wood. It is possible that nuclear bomb testing or other events have put radioactive or, for example, trace element tags into wood that can be used to verify multiplicity.
3. Locate dated old photos of dead standing BCP snags and logs laying on the ground to determine if the rate of wood decay matches what it should be if these dead pieces of wood are thousands of years old. This could offer indirect evidence of multiplicity.

Conclusion

The great ages claimed for individual BCPs are based on the assumption that the trees grew no more than one ring per year. These ‘ages’, generating a master chronology of 8,700 years, are plainly contradictory to the biblical timeframe. Upon close scrutiny there is strong evidence that multiplicity of ring formation is common under the environmental conditions where the trees grow that are used in the master chronology. Thus the assumptions behind the great ages are not correct. The number of growth rings produced by BCPs seems to be more a function of the soil water status of the area in which the BCPs grow: the drier the environment, the more rings are produced. Multiplicity of growth rings and the strip growth habit are possibly physiological mechanisms for conserving water in dry conditions. Studies that have sought to prove annularity in BCPs have not used a correct methodology or timeframe, and more suitable experimental methods have been proposed. In investigating direct evidence for multiplicity, the effect of environmental conditions needs to be accounted for. Once again, uniformitarian assumptions about the constancy of rates in the past are shown to be too simplistic, and the biblical timeframe can accommodate the data.

Acknowledgements

I wish to thank Mark Armitage for the photomicrographs in figures 5, 9, 10 and 11. Mark wasn’t given enough time to do the pictures properly, so he is not satisfied with their clarity. I think they are fantastic and thank him for them. I also thank Tom Willis, Wes Bartley and Tony Wells for their comments and suggestions on the paper.

Related articles

• Field studies in the ancient bristlecone pine forest
• Patriarchs of the forest
• Tree ring dating (dendrochronology)
• Living tree ‘8,000 years older than Christ’ (?)
• Swedish trees older than the universe?

Related resources

The Creation Answers Book

by Dr Donald James Batten, Dr David Catchpoole, Dr Jonathan Sarfati, and Dr Carl Wieland

The new and updated Creation Answers Book provides biblical answers to over 60 important questions that everyone wants to know on creation/evolution and the Bible! Not only does it answer your own questions, but equips you to effectively respond to those that resist the Gospel due to worldly teaching on origins. This important work is a ‘must have’ for anyone’s library! Includes answers to over 60 of the most-asked questions in the following 20 categories: Does God exist? Six days? Really? What about gap theories? What about carbon-14 dating? How can we see distant starlight in a young universe? What about arguments for evolution? How did bad things come about? Who was Cain’s wife? Were the ‘sons of God’ and/or the ‘nephilim’ extra-terrestrials? Was the Flood global? What about continental drift? What about all that water? How did all the animals fit on the Ark? How did fresh/saltwater fish survive? Where are all the human fossils? How could animals get to places like Australia? Were there really ice ages? How did the different races arise? What about dinosaurs? What can I do?

The Young Earth, Revised & Expanded

by John Morris

Did God create our world in six literal days, or did it evolve on its own over countless eons of time? The age of the earth—a key question in the creation/evolution debate—has been portrayed as an issue of science versus religion, but is it really that simple? The answers to these questions are vital to understanding not just earth science, but also the biblical record. Dr John Morris’ The Young Earth scientifically examines the evidence to see what the earth actually reveals about itself. This classic and definitive work, newly revised and expanded, demonstrates that the Bible can be trusted in questions of science and history. The Young Earth offers both compelling scientific analysis and effective biblical exposition. A powerful resource, it also includes a CD with PowerPoint presentations that illustrate such key concepts as salt levels in the oceans, the age of the atmosphere, the accumulations of ocean sediments and much more. Great for presentations and personal study Organized for teaching to groups of all sizes Illustrated slides illuminate important points

References

1. The White Mountains, <www.sonic.net/bristlecone/WhiteMts.html>, 17 April 2006. Return to text.
2. Glock W.S., Studhalter, R.A. and Agerter, S.R., Classification and multiplicity of growth layers in the branches of trees, Smithsonian Miscellaneous Collections 140(1):1–292, 1960. Return to text.
3. Lammerts, W.E., Are the Bristle-cone Pine trees really so old? Creation Research Society Quarterly 20(2):108–115, 1983 Return to text.
4. LaMarche Jr, V.C. and Harlan, T.P., Accuracy of tree ring dating of Bristlecone Pine for calibration of the radiocarbon time scale, Journal of Geophysical Research 78(36):8849–8858, 1973. Return to text.
5. Mirov, N.T., The Genus Pinus, Ronald Press Co., New York, 1967. Return to text.
6. Glock et. al., ref. 2 , p. 123. Return to text.
7. Ferguson, C.W. and Graybill, D.A., Dendrochronology of Bristlecone Pine: A Progress Report, Radiocarbon 25(2):287, 1983. Return to text.
8. The Ancient Bristlecone Pine, <www.sonic.net/bristlecone/Images2.html>, April 17 2006. Return to text.
9. Schulman, E., Dendroclimatic changes in semiarid America, Laboratory of Tree-ring Research—University of Arizona, University of Arizona Press, p. 137, 1956. Return to text.
10. Woomorappe J., Field studies in the ancient bristlecone pine forest, Journal of Creation 17(3):125, 2003. Return to text.
11. Woodmorappe, ref. 10, p. 126 Return to text.
12. LaMarche, V.C., Rates of slope degradation as determined from botanical evidence White Mountains, California, Geological Survey Professional Paper 352-I, 1968. Return to text.
13. LaMarche, V.C., Environment in Relation to Age of Bristlecone Pines, Ecology 50(1):56–57, 1969. Return to text.
14. LaMarche, ref. 13, p. 55 Return to text.
15. LaMarche, ref. 13, p. 57. Return to text.
16. Woodmorappe, ref. 10, p. 120. Return to text.
17. Larson, D.W., Matthes, U., Gerrath, J.A., Gerrath, J.M., Nekola, J.C., Walker, G.L., Porembski, S., Charlton, A. and Larson, N.W.K., Ancient stunted trees on cliffs, Nature 398:382–383, 1999. Return to text.
18. Oren, R. and Pataki, D.E., Transpiration in response to variation in microclimate and soil moisture in southeastern deciduous forests, Oecologia 127:549–559, 2001. Return to text.
19. Groh, B., Hubner, C. and Lendzian, K.J., Water and oxygen permeance of phellums isolated from trees: the role of waxes and lenticels, Planta 215:794–801, 2002. Return to text.
20. Schonherr, J. and Ziegler, H., Water permeability of betula periderm, Planta 147:345–354, 1980. Return to text.
21. LaMarche, ref. 13, p. 54. Return to text.
22. Glock et al., ref. 2, p. 288. Return to text.
23. Glock et al., ref. 2, p. 274. Return to text.
24. Fritts, H.C., Bristlecone Pine in the White Mountains of California: growth and ring-width characteristics, Papers of the laboratory of tree-ring research No. 4, The University of Arizona Press, p. 40, 1969. Return to text.
25. Ferguson, C.W., A 7104-year annual tree-ring chronology for Bristlecone Pine, Pinus aristata, from the White Mountains, California, Tree-Ring Bulletin 29(3–4):6, 1969. Return to text.
26. Schulman, E., Longevity under adversity in conifers, Science 119:398, 1954. Return to text.
27. Woodmorappe, J., Collapsing the long Bristlecone Pine tree ring chronologies, Proceedings of the Fifth International Conference on Creationism, 2003, p. 491. Return to text.
28. LaMarche and Harlan, ref. 4, p. 8851. Return to text.
29. Bailey, I.W., The ‘Spruce Budworm’ Biocoenose, I. Frost rings as indicators of the chronology of specific biological events, Botanical Gazette 80:97, 1925. Return to text.
30. Glock et al., ref. 2, p. 275. Return to text.