Journal of Creation 30(2):102–111, August 2018
Browse our latest digital issue Subscribe
The genetic effects of the population bottleneck associated with the Genesis Flood
Skeptics familiar with the field of genetics claim the Creation/Flood/Babel model is unrealistic in terms of population genetics and demographics. To address these claims, we created a population modelling program designed to examine changes in allele frequency within ‘biblical’ populations. Our model included an artificial genome consisting of 100,000 alleles within 40 independent chromosome arms of variable length. We start with two individuals, set their alleles to a heterozygous state (to model ‘created diversity’), and allow children to be born according to a set of predetermined population parameters. We control the average number of recombination events per chromosome arm per generation and track all alleles in all individuals. At a set year, we can introduce a ‘Flood’ by reducing the population to a single couple with three sons. Wives are assigned to these sons either by choosing randomly from available females in the population or by allowing the parental couple to produce three sisters. Population sizes of 100–500 individuals caused extreme levels of genetic drift and fixation, as expected, but these effects were minimal in populations between 4,000 and 50,000. The Flood had a demonstrable effect on reducing heterozygosity (due to inbreeding), but average fixation rates were low for moderate to large population sizes (an average of 0.76% loss with random wives, 3.07% if the wives are sisters to the parental couple’s sons). After comparing to real-world allele frequency data, we conclude that the effective population size of humanity was at one point very small and that models with small antediluvian population sizes are more likely to reflect human history. The small early population size produced a significant amount of genetic drift in the original alleles and possibly led to a significant loss of created diversity. Thus, skeptical claims that biblical models are excluded by population genetics are unwarranted.

According to Genesis, humanity started with a single man from whose side a wife was produced (Genesis 1:27, 2:21– 22). About 1,600 years later,1 a flood destroyed the earth, leaving a single family with two parents, three sons, and three daughters-in-law (DILs) of unknown relation who went on to repopulate the earth (Genesis 7:7, 8:18–19). Later, a division of the population happened at Babel; from then on people spread across the globe (Genesis 11:1–9). What many people don’t realize is that each of these events should have left a genetic signature on the modern population. Since the study of genetics is the study of how traits are passed from one generation to the next, science has given us specific tools to analyze population histories. We applied several of these tools to biblical population history.
There are several basic concepts that one must understand in order to deal with this subject. The first is called genetic drift. In small populations, random sampling of alleles each generation creates random changes in allele frequency. When populations stay small for many generations, extreme fluctuations in allele frequency can lead to allele fixation, where one allele is lost entirely and the other becomes fixed (i.e. ‘stuck’, not ‘repaired’).
The probability of an allele becoming fixed in the indefinite future is equal to the frequency of that allele in the population divided by twice the population size (because humans are diploid):
Pfix = f/2n, where f = the allele frequency and n = the population size
Ignoring new mutations (which always enter the population at a frequency of 1/2n), common alleles can easily drift to fixation in small populations. It is a mathematical certainty, given enough time. However, drift is effectively silenced in a population after it reaches a few hundred members. It would take many generations for random drift to affect allele frequencies in large populations.
Another important concept is that of created diversity. There is no reason to expect that God created Adam and Eve with no built-in heterozygosity. This actually answers a challenge issued by several critics, specifically Francis Collins, who said:
There is no way you can develop this level of variation between us from one or two ancestors,2
and his Biologos3 fellow, Dennis Venema, who said:
You would have to postulate that there’s been this absolutely astronomical mutation rate that has produced all these new variants in an incredibly short period of time. Those types of mutation rates are just not possible. It would mutate us out of existence.4
Both of their conclusions represent a superficial approach to biblical genetics. While it is true that mutation rates of that magnitude would kill us, it is only true if we have to explain all of human genetic diversity as a product of mutation. They completely ignore God-created diversity. But how much created diversity should we expect? There are about 10 million places in the human genome with two alleles (‘bi-allelic SNPs’) where both alleles are found in all major world populations.5 Since it is statistically impossible to account for these through parallel mutation, these must have existed at Babel—therefore they were on the Ark, therefore they were in Eden. If these are new mutations, they must have arisen in multiple populations independently. The statistical impossibility of this is the basis of the ‘Out of Africa’ model of human origins that posits modern humans rose from a single source population.6 The commonality of millions of alleles across world populations is the major reason modern geneticists have rejected all earlier views on the origin of races. As the well-known geneticist Lluis Quintana-Murci recently said:
But the genes that explain the phenotypic differences between populations only represent a tiny part of our genome, confirming once again that the concept of ‘race’ from a genetic standpoint has been abolished.7
There is also an additional unknown number of new mutations within the human genome. With a human population size of seven billion, it might be expected that every survivable mutation currently exists, but you would need to sequence the genomes of all seven billion people to find them. However, the less common a variation is, the more likely it is of recent origin (i.e. a mutation). Common variants occurring across populations are good candidates for created diversity, and rare variants that appear in a single population, tribe, or individual are good candidates for new mutations. We can therefore discount the rare variants without sacrificing created diversity.
The average human carries 4–5 million heterozygous alleles,8 with Africans generally having higher levels.9 Is it reasonable to assume the majority of these alleles were placed by God into Adam and/or Eve? Would not most of that initial created diversity have been lost at the Flood? How much drift and/or fixation would one expect in a Creation/ Flood/Babel scenario? Would not the inbreeding of the three post-Flood families drive humanity to extinction? Should we expect genetic homogeneity among the descendants of the Flood survivors, and is not the lack of homogeneity proof that the Flood never happened? We can answer each of these questions directly using computer programs that incorporate real-world rates for various genetic phenomena (mutation, chromosomal recombination, etc.).


Carter and Hardy created a model designed to test various models of population growth and applied it to the questions of pre-Flood, pre-Babel, and post-Exodus population sizes.10 They concluded early births are the most important factor controlling population growth. Long-lived patriarchs were basically irrelevant, because the contribution of a child to the future population is inversely proportional to the population size when the child is born. Having children late in life has little effect on the future population size. Their conclusions were important for the development of the model we will describe in this paper.
In The non-mythical Adam and Eve,11 Carter tackled claims made by Collins and Venema, who not only do not believe Adam and Eve were real historical figures but believe Adam and Eve are impossible based on what we know about human genetics. He concluded their criticisms were both unwarranted and displayed a shallow understanding of basic biblical concepts. Starting with Adam and Eve, genetic drift over time would have created an allele frequency spectrum similar to what we see today. Also, the threat of allele loss through fixation would be minimal.
But Carter’s model was overly simple. He used only 1,000 alleles, and alleles were inherited independently (i.e. no ‘linkage’). When we took that model and divided the alleles into ten distinct blocks (a simple model of chromosome arms), the results obtained were quite different. Many more alleles were lost to drift and fixation. This precipitated the current study. We simply wanted to better understand a basic question: does a Creation/Flood/Babel model reflect modern human population genetics?
Methods
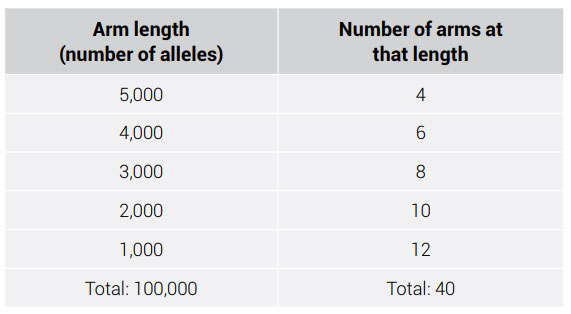
After prototyping a population model in Perl, then more advanced models in R, we implemented a full version in C for vastly improved speed and memory usage, reserving R for graphics and some data processing. We created several virtual instances on the Amazon Web Services (AWS) cloud and ran the models in bulk. An individual model takes various input parameters (table 1), based on previous work.10 We created an artificial genome by assigning 100,000 alleles to forty recombining ‘chromosome arms’, ranging in size from 1,000 to 5,000 alleles, paralleling on a reduced scale the allele density per chromosome arm in the HapMap12 data. Even though there are millions of segregating alleles in the human genome, 100,000 markers gives enough data density to see the effects of recombination in the modelled populations over many generations. Essentially, we struck a compromise between computational time and the need for more markers than the projected number of recombination events per run. Due to high levels of recombination within the centromere every generation,13 the chromosome arms are essentially independent units and the acrocentric chromosomes do not have two distinct arms. Thus there are about forty recombining units in the genome and our allele density parallels that of real human chromosomes (table 2).
Each model run starts with two individuals. We create two bitmaps with 100,000 columns and n rows, where n = a preset maximum population size. The bits in one bitmap are set to 1 for Adam and 0 for Eve, with the other bitmap arbitrarily initialized in the inverse way. Since each row represents one copy of one individual’s genome, we essentially start with 100,000 biallelic loci (more technically called ‘single nucleotide polymorphisms’, or SNPs). During each time step (‘years’), children are born, men and women marry, and old people die. Child genomes are created by taking the two genomes of each parent and randomly choosing crossover points along each modelled chromosome arm. One recombined haploid genome is passed to the child from each parent. For each chromosome arm, we randomly select between the two versions carried by the parent, copy the alleles from that chromosome up to the point of crossover, then switch to the other chromosome. For models that allow greater than one crossover per arm per generation, the algorithm simply switches to the other parental copy at each calculated crossover point. Iterating in this way through all chromosome arms and combining the results from each parent creates a diploid child genome (figure 1).
In order to simulate specific population sizes and keep computer processing and memory requirements to a reasonable level, we set a maximum population size. After reaching that predetermined size, new births caused the death of a random individual (other than the parents) already in the population. Under the standard parameters, about 5% of the individuals were replaced every year. This seems high, but the only other options were to allow the population to continue growing to infinity, to introduce controlled randomized death and/or population reduction events based on assumed causes, or keep the birth rate to levels that are unrealistically low.
To compare our results to those of real-world populations, we downloaded the most recent (Phase II, build 36), forward strand, non-redundant allele frequency statistics for three major world populations from HapMap.org.14 Populations were CEU (individuals of northern and western European descent living in Utah), YRI (Yorubas from Nigeria), and CHB+JPT (Chinese living in Beijing and Japan). After filtering to include only those variants that appeared in all three populations, data for over 3.6 million biallelic loci were obtained. For each population, the frequency of the major and minor alleles was calculated for each locus and the allele frequencies were summed and binned in intervals of 0.01.
Results
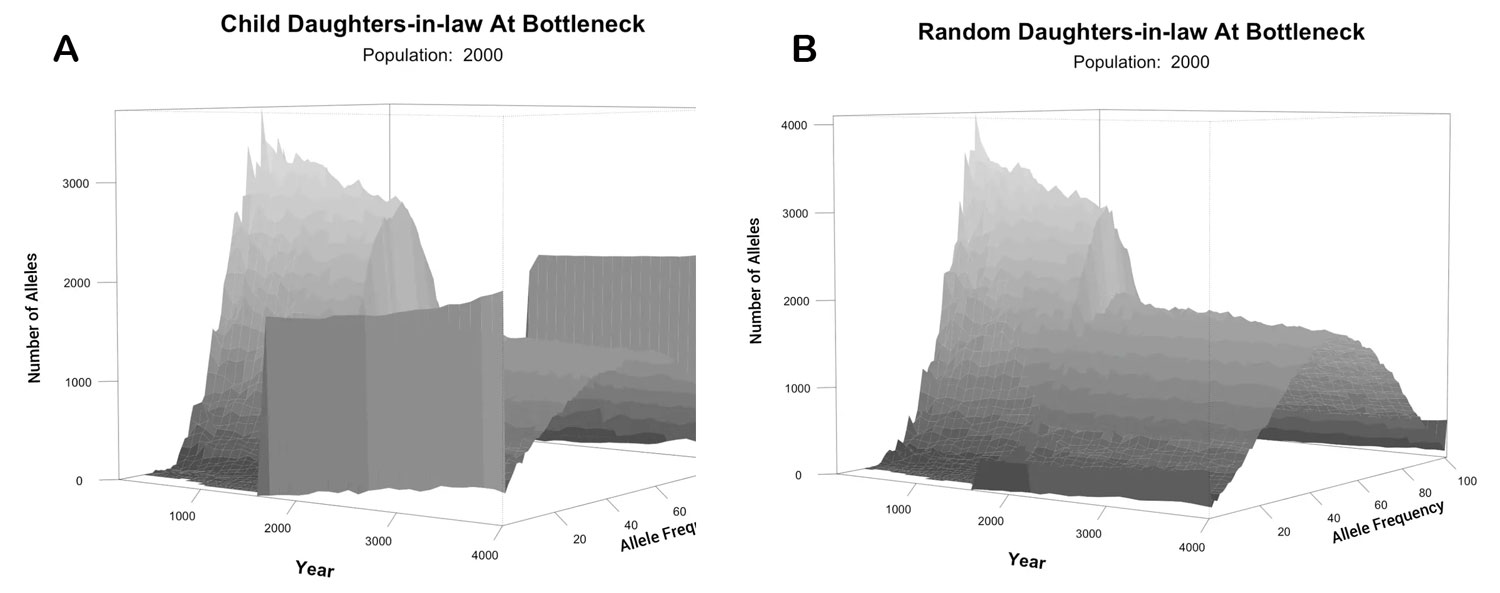
Figure 2 displays the allele frequency data for several model populations, averaged over 100 model runs (only 10 runs for n = 50,000). Population sizes were: a) 500, b) 1,000, c) 5,000, d) 50,000. A Flood-type bottleneck with random DILs occurred at year 1,600. The two wings that appear in later years among the smaller populations represent alleles that drifted to fixation (0% or 100%). There was almost no noticeable difference between the populations with 5,000 to 50,000 individuals, meaning we successfully captured the size range required to draw conclusions about any larger population size.
Changes in average population-wide heterozygosity in models with different maximum population sizes are shown in figure 3. When the population size was ≥ 3,000, heterozygosity levels were consistent and similar, and most of the loss occurred when the population was rebounding from small numbers. The average loss of heterozygosity from the Flood year to the next measurement period (100 years after the Flood) in the smallest population was 9.4%. Loss of heterozygosity in all other populations was similar, averaging 7.5%. By the time the population reached 50,000 people, the average heterozygosity had levelled out to a value of 0.427 and had not changed (to three significant figures) in 1,300 years. The slope of that line over the final 2,000 years was –3 x 10–7, meaning we would expect a –0.03% change over the next 1,000 years.
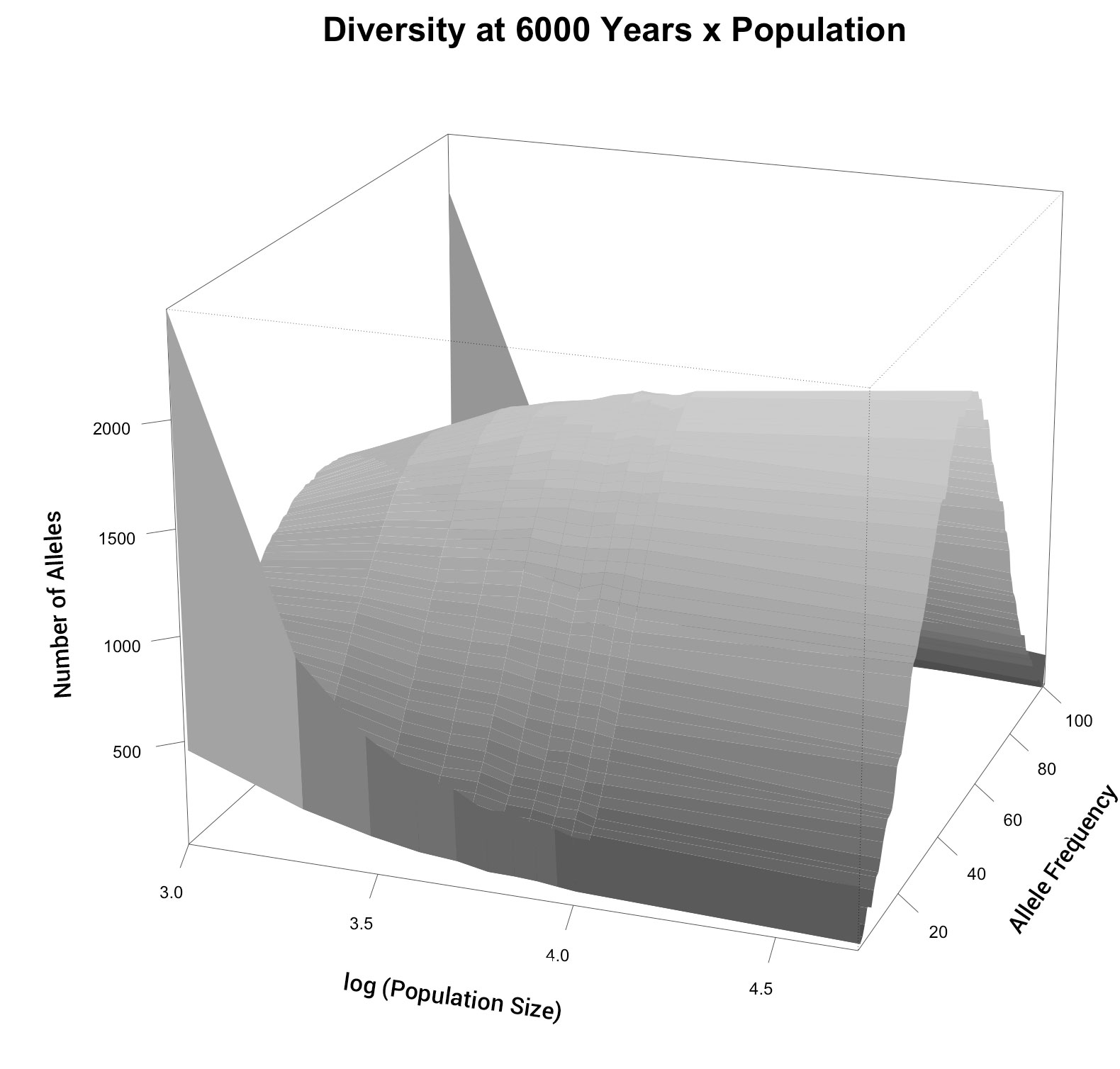
We compare the allele frequency spectrum for multiple population sizes at model year 6,000 in figure 4. As above, the larger population sizes begin to converge. In this case, a normally distributed curve centred on 0.5 was obtained. Since all alleles started at a frequency of 0.5, and since drift was expected to create variation in the allele frequencies, this was a good demonstration that our methods were producing realistic results. Models that restricted the population to less than 1,000 people had appreciable allele loss (fixation). All other populations exhibited a more-or-less normal distribution, with only slight levels of fixation.
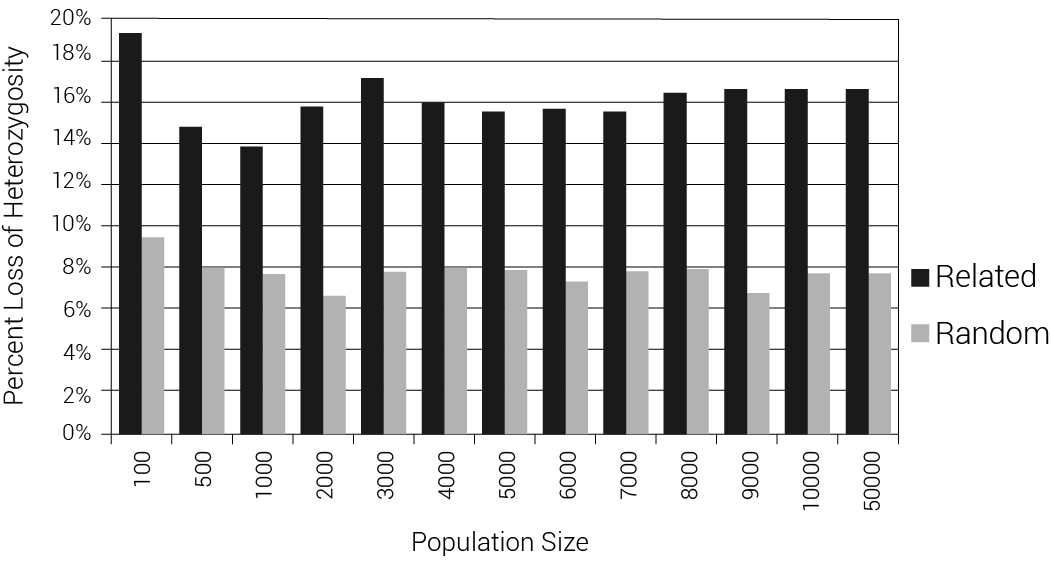
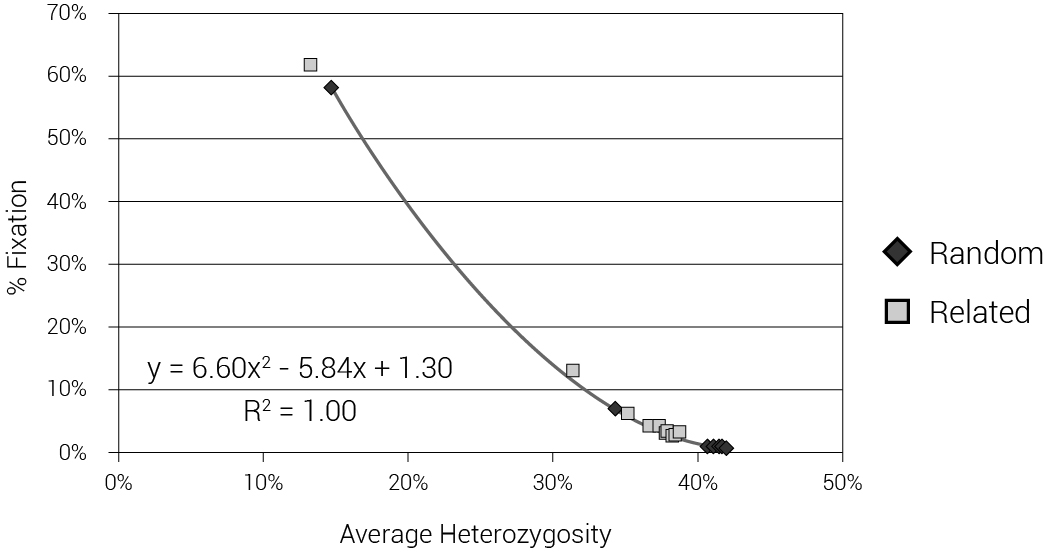
We also tested what would happen with two extreme models: one with the DILs pulled at random from the available females at the time of the Flood and one with the DILs as sisters of Shem, Ham, and Japheth. Data were taken from an average of 100 iterations for each population size of 100, 500 and 1,000 to 10,000 and 10 iterations for a population size of 50,000. We calculated the difference in mean heterozygosity between the 1,600th year, just prior to the flood event, and the 1,700th year, 100 years after the event (figure 5). Note that for the algorithm to work in small populations where it was rarely possible to find a ‘Noah’ with 6 children, some new sons and their wives had to be created during the Flood event. This figure shows an average reduction of 7.8% (for random DILs) or 16.1% (for sibling DILs) in mean heterozygosity, irrespective of population size. Figure 6 displays the allele frequency spectrum of the two modelled populations. The two ‘wings’ on each graph represent alleles that have gone to fixation (at 0% or 100% allele frequency). The models with random DILs lost 0.76% of the alleles, on average, due to fixation for population sizes between 4,000 and 50,000. In the model where the DILs were daughters of Noah, 3.07% of the alleles were lost to fixation for those same population sizes (400% higher, but still modest). We were also able to compare heterozygosity and fixation for these models (figure 7).

Since most of the loss in heterozygosity occurred when the population was small, we created models with varying population growth rates and tracked the allele frequency spectrum for 500 model years (figure 8). Fast growth led to less drift (a tighter allele frequency distribution). Slower growth created a flatter, wider curve, meaning more alleles had drifted away from their 50% starting point. In the slowest-growing population (S10/M25) it took a little less than 400 years to reach 10,000 people. This is slow compared to biological realities, so we feel the range of variables in these models span what we might expect to occur in the real world.
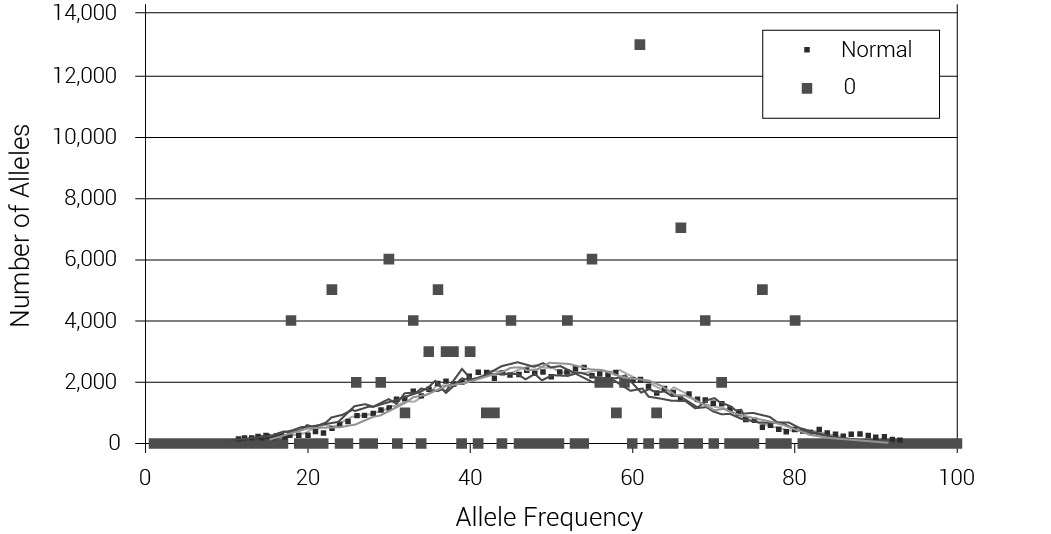
We also tested the effects of chromosome arm length on fixation and the retention of heterozygosity. No differences were found, to three significant figures, in either measure (data not shown). In order to assess the effects of recombination rate, we created models with a variable number of recombinations per arm per generation. With no recombination the allele frequency spectrum was quite erratic because there were essentially only 80 different alleles in the population, each at a different specific frequency (figure 9).
The allele frequency data for three major world populations is given in figure 10. In all three populations there are many alleles at both high and low frequencies, consistent with significant levels of drift. The average heterozygosity across the populations was 30.2%, consistent with the values generated at lower population sizes in our computer model (figure 3). It is not possible to measure fixation with these data, however, for HapMap would have skipped over any location that displays no allelic variation within, or among, contemporary populations. Figure 11 plots the relative difference for each of the 1.3 million HapMap alleles in two populations (CHB+JPT and YRI) compared to CEU. The difference in allele frequency between the European population and one of the other populations is shown along each axis. From this figure, we can see that the frequency of an allele in one population is an excellent predictor of the frequency in the other two populations. If these were created alleles, a significant amount of drift must have occurred to drive them from their expected starting frequency of 50%. Yet, since the frequency of an allele in one population is a general predictor of the frequency in another population, this is an indication that the alleles took on this frequency spectrum prior to the separation of the populations at Babel. Subsequent within-population drift caused the widening of the distribution, but note how minimal this is. The slight ridge along the JPT+CHB axis represents alleles that drifted in this population but not the other two. The dual ridge that lies on the diagonal represents alleles that drifted in the CEU population and not the others.
Discussion
We have demonstrated that a biblical population model can well account for what we see in the modern human population. In an article titled The Search for the Historical Adam that appeared in Christianity Today, the author states:
In a recent pro-evolution book from InterVarsity Press, The Language of Science and Faith, [Francis] Collins and co-author Karl W. Giberson escalate matters, announcing that ‘unfortunately’ the concepts of Adam and Eve as the literal first couple and the ancestors of all humans simply ‘do not fit the evidence’.15
We wonder exactly what evidence they are leaning on to draw these conclusions, for this study has shown that Adam and Eve can, in fact, explain the evidence we see. There is no reason to reject the biblical account based on the number of alleles in the modern human population, the distribution of those alleles, or the supposed genetic risk-factors associated with the biblical Flood.
This does not mean there is no more work to be done. Far from it, in fact. For example, our realistic population models were unable to determine the degree of loss of allelic diversity in a Creation/Flood/ Babel scenario. Since we do not know ancient human demographic history, we cannot, with certainty, say what happened to the original genes God put into Adam and Eve. However, this does not mean that modelling a range of potential options is a useless endeavor. In fact, after performing this analysis we have a much better understanding of how to explain the allelic diversity found among people today. Is it unfair of us to appeal to a limited set of explanatory models when trying to fit the data to biblical history? Hardly, for this is exactly how the Out of Africa theory developed16 and it is still common practice among evolutionists today.17
The idea that inbreeding depression would be a significant risk factor for human extinction is now moot. When we consider the number of common alleles circulating among living people, and the fact that the great majority of these are phenotypically neutral, it is not a stretch to conclude Adam and Eve carried about 10 million or more heterozygous loci and that nearly all of these have been retained in the modern human population. This depends on how many would be expected to be lost to fixation, which we estimate to be greater than 3% (the amount lost in medium to large model populations).
Genetic drift has certainly occurred, to the point where the original allele distribution has been flattened. The effect of all this drift is to make the allele frequency distribution almost appear as if the population is in mutation-drift equilibrium. This is a theoretical point at which mutations are entering the population at the same rate at which they are being removed by genetic drift, creating an allele frequency curve with many rare mutations. In other words, it is difficult to distinguish the biblical model from the evolutionary model as far as allele frequencies are concerned. What we see in contemporary humans is exactly what we would expect from an inbred or historically small population, and there is abundant opportunity for inbreeding: 1) among the ancestors of the Ark passengers prior to the Flood, 2) among the three post-Flood couples, 3) among the pre-Babel people, and 4) within the many post- Flood people groups.18 We feel the best candidate timeframe for the necessary inbreeding is that of the pre-Flood to Flood people, because there is not much time between the Flood and Babel, and because the Bible records rapid post-Flood population growth.
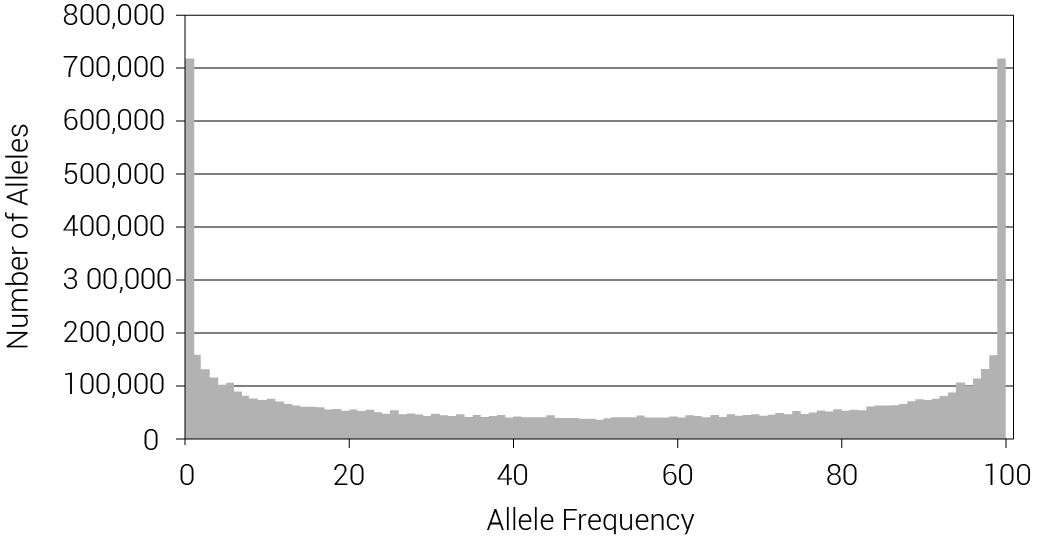
Figure 10. Combined allele frequency histogram data for three major world populations (Europeans, East Asians and Central Africans). Note that the two sides are mirror images, because for every allele at frequency n there is always a corresponding alternate allele at frequency 1-n (e.g. 0–1% equals 99–100%, etc.). There are many alleles at both high and low frequencies, but there are not many alleles in the middle range. This informs us of human demographic history, but the final distribution depends on many factors.
There is one other consideration to make before we conclude the discussion of created diversity, however: the introduction of mutations to the population prior to Babel. Most new mutations are expected to be lost to drift,19 but we have shown that drift of existing, high frequency alleles slows dramatically in exponentially growing populations. Mutational load in children increases with the age of the father (due to the fact that older men pass on gametes that have gone through many more generations/genome copying events than younger men). Thus, any child born to an ancient person could theoretically carry many genetic differences from other people. Extrapolating from the data of Crow,20 a man 500 years of age would donate approximately 10,000 mutations to a child (the current average is two orders of magnitude less than that). Kong et al. concluded that every extra year of paternity adds an average of about 2 additional mutations.21 This would mean Noah would only contribute slightly more than 1,000 mutations (40 baseline mutations + 500 years x 2) after age 500. But they also discuss models with an exponential mutational increase over time and only studied men under age 50. Either way, it could be said that Noah, by far the oldest to have fathered children recorded in biblical history, was ‘genetic poison’ to the future world population, as he would be expected to have contributed many new mutations to each of his three sons (and possibly his daughters-in-law, if they were daughters). Even though many of these alleles would have been lost to drift in the early post-Flood years, many could still exist today but most would appear as rare alleles in the mutation spectrum. This alone might explain the preponderance of alleles in the 0–1% category in figure 10. This will also be the subject of future modelling efforts.
There has been some confusion in the literature concerning created diversity and mutation. For example, Williams attributed the allelic diversity in modern humans to mutation, and perhaps conflated ‘deleterious SNPs’ with allelic diversity in general, failing to note that the bulk of common variation is phenotypically neutral and not measurably deleterious. Rare variants are more likely to be harmful (the major conclusion of the paper he cites22). He concluded, “It seems reasonable therefore to assume that something like 3 million of our SNPs have accumulated since creation”, but he derived this number by multiplying total allelic diversity (not rare allelic diversity), by the fraction calculated to be deleterious.23 He clarified things in a subsequent paper,24 but left open the possibility for a massive introduction of new mutations at or around the time of the Flood. This is an interesting possibility, but since there are only a few generations between the Flood and Babel and since recombination occurs in large chunks each generation, it would be difficult to spread millions of mutations thoroughly enough in the pre-Babel population so that they would be found in the multiple post-Babel tribes, unless they occurred very early (e.g. in Noah). This is calling for more study!
What do our conclusions mean for the rapid decline in human lifespan after the Flood? A strong bottleneck could produce a situation in which ‘longevity’ genes could be lost, as Wieland suggested.25 Since nearly all new mutations are lost to drift,26 there is little chance that a deleterious allele (or alleles) that affected lifespan was fixed in the post-Flood population. Others have demonstrated that the lifespan decline follows a tight biological decay curve and it is entirely unlikely that the author of Genesis made up numbers that so clearly represent something biological that was happening to the individuals in that population. We now know that there are multiple factors that control lifespan in humans, and people that carry significantly more of these factors tend to live significantly longer than average, even though they carry the same variants that cause disease and death in other individuals.27 There also exist areas with a significantly greater number of centenarians than average, for example people living in the highlands of Sardinia,28 the genetics of whom also happen to be associated with the original settlers on the island.29 Somehow, the loss of a certain amount of created diversity, the accumulation of new and deleterious mutations, the loss of heterozygosity in general, changes in the environment, and a likely change in epigenetic factors led to a significant decrease in human lifespan. This subject is calling for further critical inquiry.

One might wonder why we did not use an already available computer program for this project. Obviously, evolutionary population genetics programs are ill-suited to studying creation scenarios. The most comprehensive population genetics modelling program, Mendel’s Accountant,21 was written by creationists in order to address specific evolutionary claims. It has been used to measure the rate of mutation accumulation in natural populations30 and the power of natural selection (even pegging the selection coefficient for the first time ever31). Yet, ‘Mendel’ uses discrete generations: at each time interval all adults die and are replaced by their progeny. This is acceptable for large populations, but in a Creation model we need to reduce the population to small numbers with overlapping generations and so we needed to develop a platform that could handle these specific requirements. Preliminary results from an updated Mendel’s Accountant that can better model a Flood bottleneck look promising, but the update was not yet published as of the time of writing.
From the results of work done elsewhere by Carter (data not shown), chromosome arms might have 0, 1, 2, or more clear recombinations per generation, and recombinations average just over 65 per individual, per generation. Recombination is a well-known and well-characterized phenomenon controlled by the PRDM9 gene, which targets specific signal motifs in the genome.32 These motifs can degrade though mutation. It is also known that recombination rates vary across the genome and among different groups of people.33 Thus, a more detailed model that includes different rates of recombination in time- or genome-space might be able to answer questions about the difference between Africans and non-Africans, for example. But we will leave this to others and will freely share our population model (in C) upon request.34
We have established that our model produces results consistent with classic population genetics theory and that it can be used to explore alternate hypotheses of human demographic history. We believe that a small antediluvian population will create much genetic drift, and if this is followed by an exponential post-Flood growth phase, the allele frequencies will be frozen in place. Also, we would like to incorporate de novo mutations. It is quite likely that the majority of alleles in the 0–1% and 99–100% categories in figure 10 are due to pre-Babel mutations that were captured by the subsequent population growth.
References and notes
- Hardy, C. and Carter, R., The biblical minimum and maximum age of the earth, J. Creation 28(2):89–96, 2014. Return to text.
- Francis Collins speaking at the Christian Scholars’ Conference at Pepperdine University, 2011; see “Noted scientist tackles question of religious faith”, Malibu Times, 29 June 2011; malibutimes.com/articles/2011/06/29/news/news5.txt. Return to text.
- Cosner, L., Evolutionary syncretism: a critique of Biologos, 7 September 2010. Return to text.
- Haggerty, B.B., Evangelicals question the existence of Adam and Eve, National Public Radio, 9 August 2011; npr.org/2011/08/09/138957812/evangelicals-question-the-existence-of-adam-and-eve?ft=1&f=1001. Return to text.
- Frazer, K.A. et al., A second generation human haplotype of over 3.1 million SNPs, Nature 449:851–862, 2007. Return to text.
- Carter, R., The Neutral Model of evolution and recent African origins, J. Creation 23(1):70–77, 2009. Return to text.
- Quintana-Murci, L., National Centre for Scientific Research (France), Human variation chalked up to natural selection: study, PhysOrg.com, 4 Feb 2008; physorg.com/news121369077.html. Return to text.
- The 1000 Genomes Project Consortium, A global reference for human genetic variation. Nature 526:68–77, 2015. Return to text.
- Tiskoff, S.A. et al., The genetic structure and history of Africans and African Americans, Science 324(5930):1035–1044, 2009. Return to text.
- Carter, R. and Hardy, C., Modelling biblical human population growth, J. Creation 29(1):72–79, 2015. Return to text.
- Carter, R., The non-mythical Adam and Eve: Refuting errors by Francis Collins and BioLogos, 20 August 2011. Return to text.
- The International HapMap 3 Consortium, Integrating common and rare genetic variation in diverse human populations, Nature 467:52–58, 2010; www.hapmap.org. Return to text.
- Jaco, I. et al., Centromere mitotic recombination in mammalian cells, J. Cell Biol. 181(6):885–892, 2008. Return to text.
- ftp://ftp.ncbi.nlm.nih.gov/hapmap/frequencies/latest_phaseII_ncbi_b36/fwd_strand/non-redundant/. Return to text.
- Ostling, R.N., The Search for the Historical Adam, Christianity Today, 3 June 2011, pp. 23–24. Return to text.
- Carter, R., The Neutral Model of evolution and recent African origins, J. Creation, 23(1):70–77, 2009. Return to text.
- Henn, B.M. et al., Distance from sub-Saharan Africa predicts mutational load in diverse human genomes, Proc. Natl. Acad. Sci. (USA), 2015; pnas.org/cgi/doi/10.1073/pnas.1510805112. Return to text.
- Carter, R., Inbreeding and the origin of races, J. Creation 27(3):8–10, 2013. Return to text.
- Sanford, J.C. et al., Mendel’s Accountant: a biologically realistic forward-time population genetics program, Scalable Computing: Practice and Experience 8(2): 147–165, 2007. Return to text.
- Crow, J.F., The origins, patterns and implications of human spontaneous mutation, Nature Reviews Genetics 1:40–47, 2000. Return to text.
- Kong, A. et al., Rate of de novo mutations, father’s age, and disease risk, Nature 488(7412): 471–475, 2012. Return to text.
- Fu, W-Q. et al., Analysis of 6,515 exomes reveals the recent origin of most human protein-coding variants, Nature 493(7431):216–220, 2013 | doi:10.1038/nature11690. Note also that if most common variants are part of created diversity, and rare variants are more likely to cause disease, this suggests that new mutations are more deleterious than evolutionists would generally like to admit. Return to text.
- Williams, A., Human genome decay and the origin of life, J. Creation 28(1):91–97, 2014. Return to text.
- Williams, A., Healthy genomes require recent creation, J. Creation 29(2):70–77, 2015. Return to text.
- Wieland, C., Decreased lifespans: Have we been looking in the right place? J. Creation 8(2):138–141, 1994. Return to text.
- Rupe, C.L. and Sanford, J.C., Using numerical simulation to better understand fixation rates, and establishment of a new principle: Haldane’s Ratchet, Proceedings of the Seventh International Conference on Creationism, Harsh, B., Ed., Creation Science Fellowship, Pittsburg, PA, 2013. Return to text.
- Sebastiani, P. et al., Genetic Signatures of Exceptional Longevity in Humans, Science Express 0.1126/science.1190532, 1 July 2010. Return to text.
- Poulain, M. et al., Identification of a geographic area characterized by extreme longevity in the Sardinia island: the AKEA study, Experimental Gerontology 39:1423–1429, 2004. Return to text.
- Francalacci, P. et al., Low-pass DNA sequencing of 1200 Sardinians reconstructs European Y-chromosome phylogeny, Science 341:565–569, 2013. Return to text.
- Sanford, J.C. et al., Using computer simulation to understand mutation accumulation dynamics and genetic load; in: Shi, Y. et al. (Eds.), ICCS, 2007, Part II, LNCS 4488, Springer-Verlag, Berlin, pp. 386–392, 2007. Return to text.
- Sanford, J.C. et al., Selection threshold severely constrains capture of beneficial mutations; in: Marks, R.J. III et al. (Eds.), Biological Information: New Perspectives, Cornell University, New York, pp. 264–297, 2013. Return to text.
- Jeffreys, A.J. et al., Recombination regulator PRDM9 influences the instability of its own coding sequence in humans, Proc. Natl. Acad. Sci. (USA) 110(2):600–605, 2013. Return to text.
- Hinch, A.G. et al., The landscape of recombination in African Americans, Nature 476:170–177, 2011. Return to text.
- Contact: us@creation.info. Return to text.




Readers’ comments
Comments are automatically closed 14 days after publication.