Mathematics
From the mind of God

Did you know that mathematics could be racist, and that there is such a thing as ‘white math’? A claim is being made in some US academic circles that to insist that there is a correct answer to a statement like ‘2 + 2 = x’, is inherently racist, and that mathematics needs to be made antiracist. An organization1 funded by the Bill and Melinda Gates Foundation has published a document entitled, “A Pathway to Equitable Math Instruction Dismantling Racism in Mathematics Instruction“2. The document’s Letter to Reader states, “The framework for deconstructing racism in mathematics offers essential characteristics of antiracist math educators and critical approaches to dismantling white supremacy in math classrooms by visualizing the toxic characteristics of white supremacy culture … with respect to math.”
Bertrand Russell (1872–1970) a prominent anti-Christian philosopher and mathematician,3 a professed atheist,4 and Sergiu Klainerman, a professor of mathematics at Princeton University,5 among others, would disagree with the premise that mathematics is inherently racist. From a Christian perspective, we can add the fact that the basic principles of logic and mathematics cannot be racist nor are they in any way subjective human constructs, because they come from the perfect (Psalm 18:30) and holy (1 Samuel 2:2; Revelation 4:8) mind of God. Let us explore the reality that mathematics comes from the mind of God.
In Genesis 1–2, the narrator (God) uses concepts of mathematics embedded within the account without expounding the conceptual depth which underlies these concepts. For example, the enumeration of the days of Creation Week in Genesis 1 and 2 (Genesis 1:5, 8, 13, 19, 23, 31; Genesis 2:2) may appear to be rather routine. After all, we count from our earliest days—a child counts the number of days until his or her birthday. Some writers have observed that the use of the ordinal adjective (‘second’, ‘third’, etc.) with the word ‘day’ indicates that God is speaking of standard 24-hour days, and that the use of the cardinal (‘one’) and ordinals to number the days of creation demands a sequential chronological reading of the text. However, while this is true, they often fail to observe that the use of the ordinals indicates that the enumeration of the creation days is of fundamental importance. In addition, Genesis 5 implicitly uses addition, such as in the statement, “When Seth had lived 105 years, he fathered Enosh. Seth lived after he fathered Enosh 807 years and had other sons and daughters. Thus all the days of Seth were 912 years, and he died.” (Genesis 5:6–8)—i.e., 105 + 807 = 912.
Another use of a fundamental mathematical concept in Genesis 1 is the inclusion of entities in sets (e.g., six days of creative activity and “two great lights” [Genesis 1:16]). Sets are based on the abstract concept that assumes the existence of universals and not merely particulars by which each entity is viewed as independent from all others. A universal is the grouping of instances by their consistent characteristics or qualities. For example, when God later spoke to Adam and told him that he could eat from every tree in the garden, but one (Genesis 2:16–17), he used a universal to describe a set and Adam would have understood the concept to include grapes from vines, berries from bushes, and pears and nuts from trees. Universals are usually grouped into three classes: types or kinds (e.g., boats, birds, or chairs), properties (e.g., heavy, big, or small), and relations (e.g., parent, higher, colder). Since we use universals all the time, we may not understand an inherent difficulty with their existence. The problem of universals has perplexed philosophers from the earliest days.6 The challenge is how to account for their existence: Are they real? Do they exist independent of particulars? Can they exist if the universe is merely the product of random events in a material universe? Are they purely constructs of language?
The correspondence between abstractions—mathematical concepts such as ordinal counting and sets—and phenomena in nature is difficult for materialistic naturalists to explain. If mathematics is purely an invention of human minds, then it is a challenge to explain the correspondence between a mathematical equation and what happens in the natural realm.7
The efficacy of mathematics is astounding. With calculations, men and women guided the Apollo missions to the moon, can triangulate on signals generated by ‘black’ boxes to find a lost airplane at the bottom of the ocean, and can synchronize computers 20,000 kilometers apart so that they receive e-mail messages correctly. A materialistic naturalist cannot explain why pure abstractions—e.g., trigonometric equations, can have such an effect on the physical universe.
The existence of counting and mathematics is evidence that the universe was created by an intelligent designer—the God of the Bible. The laws of mathematics (e.g., commutative, associative, and distributive) come from God’s mind. Mathematics is one form of God’s thought—others include descriptive (Genesis 1), naming (Genesis 1:5), animating (Genesis 2:7), visualizing (Exodus 25:40; Exodus 26:30), and logical (Isaiah 1:18). The laws of mathematics exist in God’s mind and were not affected by the Fall of man into sin. The laws of mathematics are therefore perfect (Psalm 19:7) and can be derived without error. Of course, this does not mean that accountants and engineers (and others), affected by the Curse (Genesis 3:17–19), will always perform their arithmetical calculations without error.
Unbelievers can use the mechanics of mathematics without being able to explain what counting is or provide a logically consistent reason for why mathematics works, particularly when applied to natural systems. The problem is that their worldview claims that the universe came into existence by chance and has no non-material dimension (e.g., everlasting human souls). The fact that materialistic naturalists count and use complex mathematics to accomplish amazing things illustrates that they live in practical terms as if there is a God behind the universe, while denying His existence (Romans 1:18).8
When we examine the laws of nature (e.g., the Law of Gravitation or Coulomb’s Law of Electric Charge), we quickly discover that they are based on mathematics and that they model how God has chosen ordinarily to govern the universe; not how He must govern it—the laws of nature are descriptive, not prescriptive. The fact that nature can be described mathematically has been a continuing surprise to those who cannot think beyond their presuppositions of materialistic naturalism. They have difficulty explaining why there is a connection between physical reality and abstract mathematics. The fact that there is, indicates that the universe is more than the sum of its parts and is the product of intelligent thought.
Attributes of God are reflected in mathematics. For example:

- His infinity is hinted at by endless number sequences such as found in π (pi).
- His orderly precision and logical nature are displayed in the order and logic of mathematics, a system to which no human invention can compare. For example, the exponent in Newton’s Law of Gravitation (F = Gm₁m₂/r²) has been studied in numerous experiments and is a perfect 2 (to better than 1 part in a trillion). Also, in every right(-angled) triangle, the square of the longest side (hypotenuse) always equals the sum of the squares of the lengths of the other two sides—as expressed in the Pythagorean Theorem (a² + b² = c²).
- Similarly, his beauty can be observed through the formal symmetry and patterns in mathematics. For example, Euler’s equation eiπ + 1 = 0 combines the five most important mathematical constants into one equation.9
- His omnipresence can be seen in the correspondence between nature and mathematics. For example, we can model vocal and instrumental sounds in mathematical terms and reproduce them in our mp3 players using a digital signal processor. Or the circumference of all circles is 2πr, no matter how small or large the circle is. Both of these would be impossible if mathematics were merely an invention of man’s mind. Mathematicians did not invent math. For instance, calculus was not invented by Newton or Leibniz, it was discovered10 by them. Mathematical reality lies outside of mankind and is not invention or art, it is a study of the order God has put into the entire universe.
- His unity is seen in the system of mathematics which has order, unifying principles, rules that make sense, and an amazing interconnectedness. Clearly a deliberateness is evident in mathematics. For example, π is linked to the set of all odd numbers:
π⁄₄ = 1 – ⅓ + ⅕ – ⅟₇ + ⅟₉ – ⅟₁₁ + … (the Madhava–Leibniz formula).
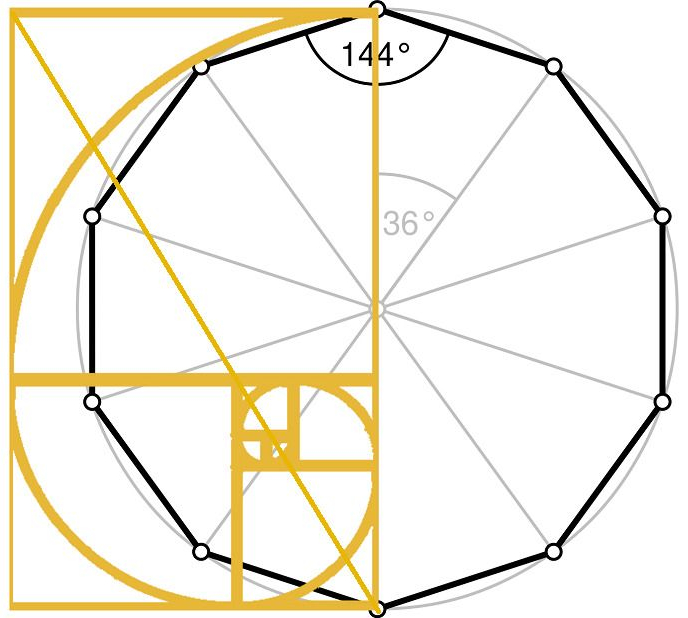
Also, ratios between consecutive numbers in the Fibonacci sequence (0, 1, 1, 2, 3, 5, 8, 13, 21 …) approach the golden ratio φ (phi). This is the number such that the equation φ² - φ - 1 = 0 gives a φ of 1.618 …, which is precisely the ratio of the radius of a circumscribing circle to the side of a regular inscribed decagon (10-sided figure). The unity of mathematics has been called ‘remarkable’, ‘surprising’, ‘unexpected’, ‘mysterious’, ‘a miracle’, and ‘astonishing’, by those who have no belief in God. - While God’s unity is seen in mathematics, so also is his diversity (in a Trinity)—in a single system that can be used to describe human behaviour, calculate stresses on a building foundation, predict hurricane behaviour, and model the revolution of the planets.
- The fact that God is a communicator is shown through mathematics’ ability to provide complex, specified information such as is evidenced when vocal and instrumental sounds in a musical presentation can be represented in mathematical terms, stored in digital form (zeros and ones), and reproduced again in analog form as puffs of air with high fidelity, using computer chips called digital signal processors.
- His power is demonstrated through what can be accomplished with mathematics—to synchronize traffic flows, describe musical scores that stir the heart, and define monetary systems that allow modern economies to function.
- His truthfulness is observed in the constancy of equations such as 2 + 2 = 4. Since all truth is ultimately God’s truth, anything which is true reflects God’s nature.
- God’s consistency (unchangeableness) is shown from the fact that the results of calculations applying mathematical equations will never change anywhere in the universe. The fact that even atheists believe in the consistency of mathematics is evidenced by advocates of SETI (Search for Extra-Terrestrial Intelligence) who expect that someday we will receive a radio signal from outer space that is based on a regular pattern such as counting by binary numbers.

Only people with a Christian worldview can understand that mathematics reflects the logical, ordered, and good mind of God. As one of His forms of thought, God thinks mathematically. So, the existence of mathematics declares to mankind that God is behind the order in the universe. We can count and perform mathematical calculations because we are image-bearers of God, (Genesis 1:26–27) and can think God’s thoughts after Him. The notions that there are such things as ‘white math’ and that mathematics is ‘racist’ is utter foolishness (Romans 1:22), as is any idea that mathematics is a mere human construct or invention. In addition, such an approach to mathematics, which eliminates the demand for precision and objectivity, is a disservice to those who can benefit from learning to apply mathematics correctly.
References and notes
- Math Equity Toolkit; equitablemath.org. Return to text.
- https://equitablemath.org/wp-content/uploads/sites/2/2020/11/1_STRIDE1.pdf. Return to text.
- Bertrand Russel, The Principles of Mathematics; Cambridge University Press, 1903; people.umass.edu. Return to text.
- “The right answer”, posted on The Atheist Conservative; theatheistconservative.com Return to text.
- Sergiu Klainerman, There Is No Such Thing as “White” Math,bariweiss.substack.com, 1 Mar 2021. Return to text.
- The Medieval Problem of Universals, plato.stanford.edu, 31 Oct 2017. Return to text.
- Vern S. Poythress, A Biblical View of Mathematics, 4 Jun 2012; frame-poythress.org. Return to text.
- Vern Poythress, Creation and Mathematics; or What Does God Have to do with the Numbers? frame-poythress.org, 21 May 2012. Return to text.
- Other examples of beauty in mathematical equations are provided by Clara Moskowitz, The 11 Most Beautiful Mathematical Equations, livescience.com, 1 Jun 2017. Return to text.
- Ramos, S.C., The Discovery of Calculus: Leibniz vs. Newton; stmuhistorymedia.org, 3 Nov 2017. Return to text.




Readers’ comments
Comments are automatically closed 14 days after publication.