Journal of Creation 33(1):102–109, April 2019
Browse our latest digital issue Subscribe
Have uniformitarians rescued the ‘Pacemaker of the Ice Ages’ paper?
The current dominant Ice Age explanation is the astronomical, or Milankovitch, theory. This theory posits that slow changes in Earth’s rotational and orbital motions ‘pace’ the timing of ice ages by modulating the manner in which solar radiation incident on the earth is distributed with season and latitude. This theory is widely accepted because of an influential 1976 paper entitled “The Pacemaker of the Ice Ages”. However, the paper’s results were critically dependent upon an assumed age for the most recent geomagnetic reversal, an age which even uniformitarian scientists no longer accept as valid. If one re-does the calculations using the new uniformitarian age assignment, the results are greatly weakened. Although additional evidence for the Milankovitch theory seems weak, a 1997 paper seems to ‘rescue’ the results of this iconic paper. However, this ‘rescue’ may be influenced by ‘selection bias’ and arguably requires arbitrary, capricious handling of seafloor sediment data. Hence, these 1997 results are not terribly convincing.

In 2016 I published a paper showing that the well-known “Pacemaker of the Ice Ages” paper, which convinced many uniformitarians of the validity of Milankovitch climate forcing, depended upon an assumed age of 700 ka for the most recent geomagnetic reversal (the Brunhes-Matuyama magnetic reversal), despite the fact that uniformitarian scientists now claim that its age is 780 ka.1-3 The Pacemaker authors never explicitly stated that they were assuming the age of the Brunhes-Matuyama (B-M) reversal to be 700 ka, but a careful reading of both the Pacemaker paper itself and a 1973 paper by Nicholas Shackleton and Neil Opdyke clearly shows this to be the case. 2,4
In my article, I replicated the ‘frequency domain’ analysis of the original Pacemaker paper and then showed that this age revision adversely affected the published Pacemaker results.5,6 I also showed a method by which laypeople could verify that the most important results were at least approximately correct.7 An even more thorough re-analysis, taking into account further revisions to the data, undermined these results even further.8
Creation and secular researchers have long pointed out serious difficulties with the Milankovitch theory.9-12 In spite of these difficulties, many uniformitarians accept the theory largely because of analyses of paleoclimate data like that in the Pacemaker paper:
“In fact, the evidence for the role of astronomy [in climate variation] comes almost exclusively from spectral analysis. The seminal paper was published in 1976, titled, ‘Variations of [sic] the earth’s orbit: pacemaker of the ice ages’ (Hays et al., 1976).”13
Largely because of the Pacemaker paper, uniformitarian scientists generally assume the Milankovitch theory to be correct and use that assumption to date sediment and ice cores in a process called ‘orbital tuning’.14 Uniformitarian scientists even use orbital tuning to calibrate argon-argon dating standards.15 Obviously, without objective evidence to support the theory, hundreds, if not thousands, of uniformitarian age assignments are suspect, even by uniformitarian reckoning.
To the best of my knowledge, there has been no public response to my research from uniformitarian scientists or old-earth creationists. However, one paper seems to ‘rescue’ the Pacemaker results, so I feel it is important to address it. This 1997 paper, entitled “The timing of major climate terminations”, was authored by paleoclimatologist Maureen Raymo.16
Background
Secular paleoclimatologists now claim that there have been about 50 ice ages (‘glacial intervals’) during the Pleistocene (within the past 2.6 Ma).17 This claim is clearly not based on geological field evidence. Even if one accepts the claim of multiple ice ages, interpretation of the field data is complex,18 and glaciers in the most recent ice age would likely bulldoze and destroy much of the evidence for previous ice ages. Likewise, the geological field data do not demand multiple Pleistocene ice ages. For instance, even some secular geologists acknowledge that there is strong geological evidence in western Alberta for only the most recent ice age, which creationists would argue was the only Ice Age.19

Instead, this claim of 50 Pleistocene ice ages is based upon a Milankovitch interpretation of seafloor sediment oxygen isotope ‘wiggles’. For instance, Lisiecki and Raymo constructed a composite ‘stack’ of benthic δ18O values from 57 deep-sea sediment cores which supposedly extended back 5.3 Ma.20 If you plot just the Pleistocene part (the most recent 2.6 Ma) of this composite stack (figure 1), there are about 50 wiggly cycles. Hence, secular paleoclimatologists claim there have been 50 Pleistocene ‘glacial’ intervals.
Secular paleoclimatologists use a ‘numbering system’ called Marine Isotope Stages (MIS) to identify similar oxygen isotope patterns in different sediment cores. Generally, but with some exceptions, odd-numbered MIS correspond to presumed warmer ‘interglacials’, and even-numbered MIS correspond to presumed colder ‘glacials’. Different MIS are separated by ‘boundaries’, generally located at places where the oxygen isotope values transition from a local maximum to a local minimum.21 If the oxygen isotope values transition between an extreme local maximum and an extreme minimum value, then the boundary is called a ‘termination’.22
A 1973 paper by Shackleton and Opdyke used oxygen isotope data from a far western Pacific core designated as V28-238 and an assumed age of 700 ka for the B-M reversal boundary, to assign tentative ages to 21 MIS boundaries, three of which were used in the Pacemaker paper.4,2
Since the age of the B-M reversal has since been revised to 780 ka, use of Shackleton and Opdyke’s method, as well as the methodology of the Pacemaker authors, yields age estimates for the MIS boundaries that are too old to be consistent with the currently accepted version of the Milankovitch theory.
This means that this key argument for Milankovitch climate forcing is also invalid. That, in turn, means that hundreds (if not thousands) of orbitally tuned secular age assignments are in doubt, even by uniformitarian reckoning.
Given this state of affairs, one would not be surprised if uniformitarian scientists had at some point attempted to ‘prove’ that the currently accepted ages for the MIS boundaries are still correct, despite the fact that the method originally used to obtain those ages is invalid. This would enable them to claim that the Pacemaker results no longer depend on Shackleton and Opdyke’s 1973 calculations, which would mean that those results may still be used as confirmation of the astronomical theory. Regardless of whether or not this was Raymo’s intent, her 1997 paper appears to fill this purpose.
Raymo’s methodology
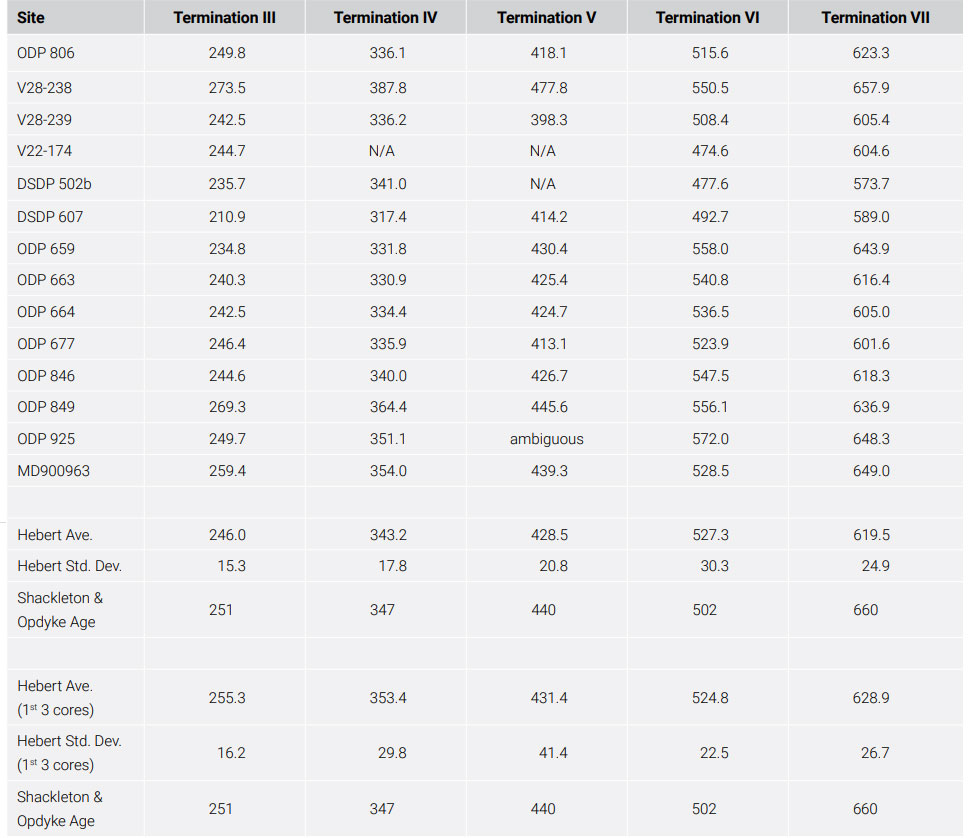
Raymo used 11 oxygen isotope (δ18O) seafloor sediment records containing the B-M reversal boundary to determine the ages for several ‘terminations’. She used the age assignment of ~780 ka for the B-M boundary, as well as two other radioisotope age assignments, to set up simple, ‘untuned’ timescales, i.e. timescales which did not necessarily assume the Milankovitch theory to be correct, for these eleven δ18O records. One of these age assignments was 13.5 ka for the Marine Isotope Stage (MIS) 2.0 boundary, also known as Termination I. The second was an age assignment of 128 ka for the MIS 6.0 boundary, also known as Termination II. The third control point was MIS boundary 19.0, which was assumed to be 6 ka younger than B-M reversal boundary. Since the age of the B-M reversal boundary was taken to be 778 ± 3.5 ka, she took the age of MIS 19.0 to be 772.2 ka. She assumed constant sedimentation rates between these three age assignments, as a first approximation, in order to set up the untuned timescales. After doing so, she obtained average estimated ages for Terminations III, IV, V, VI, and VII (MIS boundaries 8.0, 10.0, 12.0, 14.0, and 16.0, respectively). When she did so, the ages obtained for these five Terminations agreed fairly well with the age assignments obtained by orbital tuning. Raymo thus saw these results as a confirmation of the orbitally tuned SPECMAP timescale. Uniformitarians now acknowledge that the SPECMAP timescale was seriously inaccurate for (presumed) ages greater than 600 ka, although they think it is accurate for the more recent past.23 Because Raymo’s results concerned these more recent (and presumably correct) ages, they are worth discussing here.
Of particular interest are the age assignments for Terminations III and V (MIS boundaries 8.0 and 12.0, respectively), as these were the age assignments the Pacemaker authors used, along with the age of 127–128 ka for the Termination II boundary (MIS 6.0) to set up their preliminary ‘SIMPLEX’ and ‘PATCH’ timescales. Raymo obtained a mean age estimate of 247.9 ka (standard deviation of 10.0 ka) for the MIS 8.0 boundary and a mean age estimate of 423.6 ka (standard deviation of 13.6 ka) for the MIS 12.0 boundary (table 1). By comparison, the Pacemaker paper used age estimates of 251 and 440 ka, respectively, for these MIS boundaries.

Selection bias?
However, there may have been some ‘selection bias’ in Raymo’s choice of sediment cores, as she did not use all the available cores for her analysis. She excluded three sediment cores used to obtain the SPECMAP tuned timescale, even though these three cores also contained the B-M magnetic reversal. These were the V28-238 core, the DSDP 502 core off the coast of Central America, and the V22-174 core in the southern Atlantic. She excluded these cores because they had already been orbitally tuned and used to obtain the SPECMAP timescale. However, this does not seem like a sufficient justification for their exclusion. As long as one still has the original δ18O data as a function of depth, it is certainly possible to ‘untune’ those sediment records and to then treat them like any other sediment cores. Hence Raymo could have used her methodology to obtain termination age estimates from the untuned δ18O records in these three cores. Hence, it still seems odd that Raymo excluded them from her analysis. This is especially true for the V28-238 core. This core supposedly had a nearly constant sedimentation rate,24 and it played a critical role in the Pacemaker paper, as this was the sediment core used by Shackleton and Opdyke in their 1973 analysis.4,2 In fact, the V28-238 core was so important to uniformitarian scientists that they dubbed its oxygen isotope record an ice age ‘Rosetta Stone’!25 Even though secular scientists later claimed that there was a significant discontinuity within the V28-238 core, it is possible to correct for that supposed discontinuity, and other uniformitarian scientists have done so.26 Hence, Raymo still should arguably have included it in her analysis.
Apparently, the V28-238 core has ‘outlived its usefulness’. Once hailed as an ice age ‘Rosetta Stone’, it now seems to be just another ‘run-of-the-mill’ sediment core, no more important than any other of the thousands of cores in existence. Interestingly, I have never been able to find an explicit statement of why uniformitarian scientists believed that the sedimentation rate within the V28-238 core was nearly constant. One can’t help but wonder if this assumption was based on circular reasoning. Did uniformitarian scientists conclude that the V28-238 sedimentation rate was nearly constant because its oxygen isotope values were behaving in a fashion roughly consistent with Milankovitch assumptions? If so, they may have reasoned that variations in the sedimentation rate would have distorted this signal. Since they ‘knew’ (or strongly suspected) that the Milankovitch theory was correct, they may have viewed this ‘idealized’ δ18O behaviour as confirmation of a nearly constant sedimentation rate within the V28-238 core.
Also, there are at least seven other sediment cores, also containing the B-M reversal boundary, which had already been used to ‘confirm’ the age of 780 ka for the B-M reversal boundary.27 Moreover, this confirmation was published in 1996, just one year prior to Raymo’s paper. Since Raymo was accepting this age assignment of 780 ka as a ‘given’, it is not clear why she excluded these seven cores from her analysis. Raymo stated:
“Not included in this study are cores with unspliced core breaks, low sampling resolution, drilling disturbance, hiatuses, and/or poorly resolved or missing isotopic events.”28
Presumably Raymo excluded the other seven cores because they were characterized by these defects. But if that is the case, why then were they used in the 1996 paper to ‘confirm’ the age of 780 ka for the B-M reversal? If these defects precluded their use in Raymo’s study, shouldn’t those same defects have precluded their use in the 1996 study?
There could in fact be many more sediment cores containing the B-M reversal boundary in addition to these seven, which were listed in a single paper. Inclusion of these additional sediment cores would have increased the size of Raymo’s sample and could have yielded results less favourable to Milankovitch expectations. It is tempting to redo Raymo’s calculations, after including all known sediment cores containing the B-M magnetic reversal boundary, but candidly, I do not presently have the time or energy to ‘hunt’ for all these data cores and to perform such an analysis. However, I did re-do her calculations for the ages of the terminations after including the three SPECMAP cores that she excluded (table 2). In obtaining the average age estimates for each termination, I gave ages from each core equal weight. Including the age estimates from these three cores generally increased the ‘spread’ in the age estimates. Of particular interest are the age estimates obtained from the first three cores in table 2, the V28-238, V28-239, and ODP-806 cores. These three cores are located very close to one another in the far western Pacific. Hence, one might expect all three cores to yield similar age estimates for the MIS boundaries, with a smaller standard deviation than that obtained using all 14 cores. In fact, the standard deviation for these three cores were generally larger than those obtained for the whole set. Interestingly, the standard deviation for Termination V (MIS 12.0) obtained from these three cores (41.1 ka) is twice that obtained from the whole set (20.8 ka).

It is also worth noting that Raymo stated that she used records that “exhibit the typical sequence of oxygen isotope stages with no obvious hiatuses, drilling disturbance, or large swings in sedimentation rates [emphasis added].”28 This itself may have been a subtle example of selection bias—what does a ‘typical’ oxygen isotope record look like? Uniformitarian scientists think that an ideal, undistorted oxygen isotope record shows a ‘sawtooth’ pattern, indicative of slow buildup of the ice sheets, followed by rapid collapse of those ice sheets. For instance, see figure 2, which shows the most recent part of the SPECMAP orbitally tuned oxygen isotope record, plotted as a function of (uniformitarian) time. If one compares the uppermost 12.5 m of Raymo’s oxygen isotope graphs (plotted as a function of depth) in her figure 1 with a graph of the SPECMAP oxygen isotope record, plotted as a function of time, there is a striking similarity. In other words, assumed uniformitarian age is roughly proportional to depth if one uses sediment cores containing the ‘expected’ δ18O pattern. Hence, by choosing cores whose δ18O records (in the spatial domain) generally looked like the SPECMAP δ18O record (in the time domain), she may have unconsciously biased the results to agree with the SPECMAP timescale. As of 26 September 2018, Raymo’s paper can be freely accessed online.29
Remember also that the very choice of which peak or trough is designated as a particular MIS δ18O feature is somewhat subjective. Since secular paleoclimatologists are expecting the MIS boundaries to occur at certain relative depths/times, they will choose MIS features that already correspond to their expectations.
So, do Raymo’s results salvage the Pacemaker paper?
Salvaging the Pacemaker results?

Superficially, it seems that they do. Raymo did not actually reperform the Pacemaker analysis using these new age assignments. However, one can use the ‘shortcut’ method described previously to estimate the effect that these age revisions would have on the original Pacemaker results. Her age estimate for the MIS 12.0 boundary could easily be (plus or minus one standard deviation) as low as 410 ka or as high as 437 ka. Remember that she also took the age of the MIS 6.0 boundary to be 128 ka.

If one uses the versions of the core data used in the original Pacemaker paper (yes, multiple versions of some of the same data sets exist!), then the results from the shorter RC11-120 core would be essentially unaffected, as the age estimate of 128 ka for the MIS 6.0 boundary is almost identical to the age estimate of 127 ka used by the Pacemaker authors. Likewise, if one uses the higher age estimate of 437 ka for the MIS 12.0 boundary, the results for the longer E49-18 core will be very similar to the results that the Pacemaker authors obtained using an age estimate of 440 ka for this boundary. If one uses an age of 410 ka for this boundary, then one can show that the total time assigned to the E49-18 core will be 358 ka, which is 90% of the original time of 363 ka that the Pacemaker authors assigned to it. This means that the periods obtained from spectral analysis of the core data will be about 90% of the periods reported in the Pacemaker paper. Since most of the periods for the E49-18 core were on the ‘high’ side, this actually improves the E49-18 spectral results, bringing them into closer agreement with Milankovitch expectations.

Likewise, re-performing the spectral analysis for the so-called ‘PATCH’ composite data sets yields good agreement with Milankovitch expectations when one uses SPECMAP ages for the relevant MIS boundaries (figures 3, 4, and 5). Furthermore, the results are generally statistically significant. Of course, since the SPECMAP timescale is orbitally tuned, it implicitly assumes the validity of the Milankovitch theory. Hence, agreement with the theory is hardly surprising.
Of course, these results salvage the Pacemaker paper only if one ignores the issues raised above.
Shedding light on the issue
Of course, uniformitarians could bring some real clarity to this issue if they would simply state clearly, and on-the-record, whether they still think the sedimentation rate for the V28-238 core was nearly constant. One strongly suspects that they will not do so, because either a yes or no answer is problematic for them. If they say yes, then by their reckoning the methodology used in the Pacemaker paper is still valid, but they need to re-do the Pacemaker results taking into account the age revision to the B-M reversal boundary. I have already shown that this revision adversely affects the Pacemaker results, and even more so when one removes an ostensibly ‘stretched’ 30 cm core section.6,8 Likewise, a constant sedimentation rate for the V28-238 core would imply that Raymo should have used it in her analysis and arguably should have given greater statistical weight to the (untuned) age estimates she obtained from it. On the other hand, if they answer no, they are tacitly acknowledging that the methodology used explicitly in Shackleton and Opdyke’s 1973 paper, and implicitly in the 1976 Pacemaker paper, was flawed from the beginning. In that case the Pacemaker paper should never have been published in the first place! Of course, without the Pacemaker paper, there would have been no justification for orbital tuning, nor for an orbitally tuned SPECMAP timescale, nor for an after-the-fact ‘confirmation’ of that SPECMAP timescale.
‘Confirmation’ of the revised reversal age?
Uniformitarians claim that radioisotope dating ‘confirmed’ the new age of 780 ka for the B-M reversal boundary, but this claim is not terribly convincing.30-32 By 1979 uniformitarians had already revised the age of the B-M reversal from 700 to 730 ka. They based this revision on revised K-Ar decay constants and an increase in available data, so this revision does not appear to have been motivated by circular reasoning per se.33 However, in the early 1990s uniformitarian scientists arbitrarily overruled this age estimate of 730 ka for the B-M reversal boundary, recommending that it be changed to 780 ka.3,34 The motivation for this revision was apparently to ‘protect’ the Milankovitch theory from falsification. Uniformitarian scientists were attempting to ‘orbitally tune’ sediment data from other sediment cores and were apparently having difficulty doing so, given the then-accepted ages for the most recent magnetic reversals, including the B-M reversal. This is actually rather remarkable, because the orbital tuning process usually gives considerable ‘wiggle room’ (pun intended!) to the tuner. Even computer-generated random wiggle patterns have been successfully tuned to the Milankovitch theory, even though the computer-generated wiggle patterns had nothing to do with the real world!35,36 Rather than simply conceding that the Milankovitch theory was incapable of fitting all the available data, they revised upward the ages for the most recent reversals, including the B-M reversal. That revision is definitely an example of circular reasoning!
However, uniformitarians soon claimed that this new age of 780 ka for the B-M reversal boundary was ‘confirmed’ by K-Ar dating.37 Yet one can’t help but suspect that the Milankovitch theory was subtly influencing their analysis of the data. For instance, uniformitarians obtained their 1979 age estimate of 730 ka for the B-M reversal (as well as two other reversals) using K-Ar ages for volcanic rocks containing magnetic reversal data. The authors used a statistical technique that minimized inconsistencies in the estimated dates for the magnetic reversals.32 One of the papers ‘confirmed’ the new age estimate of 780 ka using the same method, but after including higher age estimates excluded from the original 1979 analysis.30 The inclusion of these higher ages naturally ‘nudged’ the age of the B-M reversal to a higher value, thereby ‘confirming’ the new estimate!
Of course, this change to the age of the B-M reversal boundary endangered the original Pacemaker results, without which there was no justification for orbital tuning in the first place!
How firm a foundation—or not
One gets the impression that uniformitarians have been handling the seafloor sediment data in a rather capricious and arbitrary manner. One also gets the impression that they are simply unwilling to allow the Milankovitch theory to be falsified.
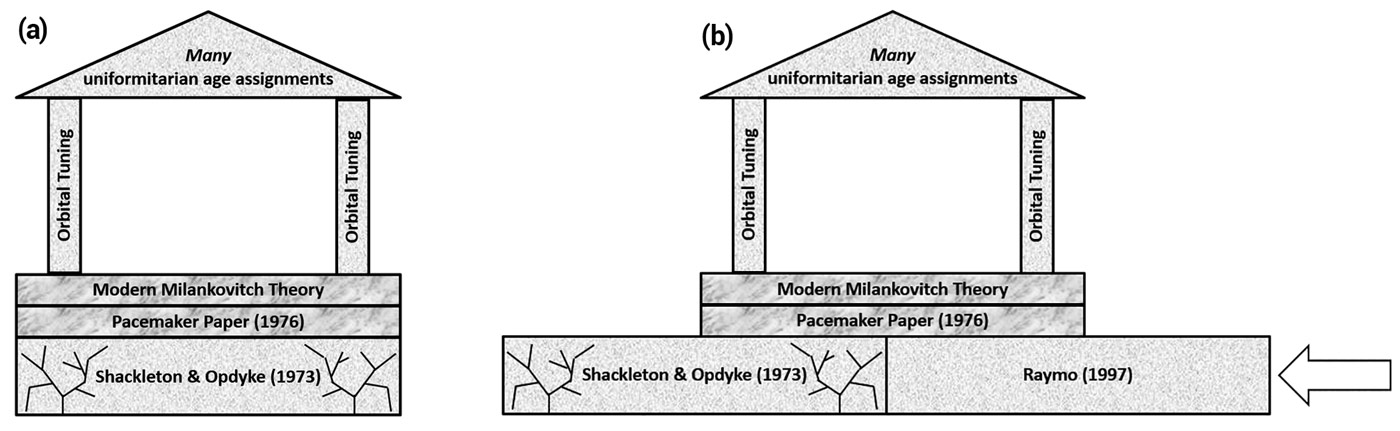
Although Raymo does not explicitly mention the adverse effect that the B-M age revision has on the Pacemaker results, she does allude to concerns that orbital tuning involves ‘bias’, i.e. circular reasoning.38 Reading between the lines, one can’t help but wonder if the 1997 Raymo paper, published just five years after K-Ar dating supposedly ‘confirmed’ the new age of 780 ka for the B-M reversal, was an attempt at ‘foundation repair’ for the Pacemaker paper (figure 6). The Pacemaker results rested on the results of Shackleton and Opdyke’s 1973 paper. With those results invalidated, uniformitarians had an obvious need to ‘prop’ up the Pacemaker paper in order to prevent the entire orbital tuning enterprise from collapsing into a heap of ruins!
Whether or not one considers Raymo’s ‘confirmation’ of the SPECMAP timescale to be convincing depends largely upon one’s bias. Obviously, as a creation researcher, I am strongly biased against the Milankovitch theory and the SPECMAP timescale. However, I can’t help but wonder how others, including uniformitarians who are not necessarily convinced of the Milankovitch theory, would view this apparent ‘after-the-fact’ justification for the Pacemaker results. How would he respond if a Milankovitch enthusiast were to candidly tell him:
“The original confirmation of the Milankovitch theory was flawed because we later changed an age estimate that was crucial to the results. In fact, we changed this age estimate because we were having trouble reconciling other data with the Milankovitch theory, so rather than simply admit the theory was wrong, we overruled our own radioisotope age estimates in order to make the data ‘fit’ the theory. But it’s OK now, because we have since managed to justify the original results using data from other sediment cores, twenty-one years after the fact!”
Of course, when one puts it like that, it sounds rather silly, which is perhaps why we don’t see such candid admissions by Milankovitch proponents in the technical literature!
References and notes
- Hebert, J., Revisiting an iconic argument for Milankovitch climate forcing: should the ‘Pacemaker of the Ice Ages’ paper be retracted?—part 1, Answers Research J. 9:25–56, 2016. Return to text.
- Hayes, J.D., Imbrie, J., and Shackleton, N.J., Variations in the earth’s orbit: Pacemaker of the ice ages, Science 194 (4270):1121–1132, 1976. Return to text.
- Shackleton, N.J., Berger, A., and Peltier, W.R., An alternative astronomical calibration of the lower Pleistocene timescale based on ODP Site 677, Transactions of the Royal Society of Edinburgh: Earth Sciences 81(4):251–261, 1990. Return to text.
- Shackleton, N.J. and Opdyke, N.D., Oxygen isotope and palaeomagnetic stratigraphy of Equatorial Pacific Core V28-238: oxygen isotope temperatures and ice volumes on a 105 Year and 106 Year Scale, Quaternary Research 3:39–55, 1973. Return to text.
- Hebert, J., Revisiting an iconic argument for Milankovitch climate forcing: should the ‘Pacemaker of the Ice Ages’ paper be retracted?—part 2, Answers Research J. 9:131–147, 2016. Return to text.
- Hebert, J., Revisiting an iconic argument for Milankovitch climate forcing: should the ‘Pacemaker of the Ice Ages’ paper be retracted?—part 3, Answers Research J. 9:229–255, 2016. Return to text.
- Hebert, J., A broken climate pacemaker?—part 1, J. Creation 31(1):88–98, 2017. Return to text.
- Hebert, J., The ‘Pacemaker of the Ice Ages’ paper revisited: closing a loophole in the refutation of a key argument for Milankovitch climate forcing, CRSQ 54:133–148, 2017. Return to text.
- Cronin, T.M., Paleoclimates: Understanding climate change past and present, Columbia University Press, New York, pp. 130–139, 2010. Return to text.
- Oard, M.J., Astronomical troubles for the astronomical hypothesis of ice ages, J. Creation 21(3):19–23, 2007. Return to text.
- Winograd, I.J., Coplen, T.B., Landwehr, J.M. et al., Continuous 500,000-year climate record from vein calcite in Devils Hole, Nevada, Science 258(5080):255–260, 1992. Return to text.
- Muller, R.A. and MacDonald, G.J., Spectrum of 100-kyr glacial cycle: orbital inclination, not eccentricity, PNAS 94:8329–8334, 1997. Return to text.
- Muller, R.A. and MacDonald, G.J., Ice Ages and Astronomical Causes: Data, spectral analysis and mechanisms, Praxis Publishing, Chichester, UK, p. xiv, 2000. Return to text.
- Hebert, J., The dating ‘pedigree’ of seafloor sediment core MD97-2120: a case study, CRSQ 51(3):152–164, 2015. Return to text.
- Hebert, J., Circular reasoning in the dating of deep seafloor sediments and ice cores: the orbital tuning method, Answers Research J. 7:297–309, 2014. Return to text.
- Raymo, M.E., The timing of major climate terminations, Paleoceanography 12(4):577–585, 1997. Return to text.
- Walker, M. and Lowe, J., Quaternary science 2007: a 50-year retrospective, J. Geological Society, London 164:1073–1092, 2007. Return to text.
- Oard, M.J., An Ice Age Caused by the Genesis Flood, Institute for Creation Research, El Cajon, CA, pp. 135–139, 1990. Return to text.
- Oard, M.J., Only one glaciation observed in western Alberta, Canada—the ice-age reinforcement syndrome, J. Creation 29(2):12–13, 2015. Return to text.
- Lisiecki, L.E. and Raymo, M.E., A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography 20, PA1003, 2005. Return to text.
- Gibbard, P.L., Climatostratigraphy; in: Elias, S.A. (Ed.), Encyclopedia of Quaternary Science, Elsevier, Amsterdam, pp. 2819–2825, quoted in modified form by the INQUA Commission on Stratigraphy and Chronology, 2007, inqua-saccom.org/stratigraphic-guide/climatostratigraphy-geological-climate-stratigraphy/, accessed 23 April 2015. Return to text.
- Broecker, W.S., Terminations, in Milankovitch and Climate, part 2, Berger A., et al. (Ed.), D. Reidel Publishing, Norwell, MA, pp. 687–698, 1984, cited in Raymo, ref. 16. Return to text.
- Muller and MacDonald, ref. 13, pp. 149–150. Return to text.
- Shackleton, Berger, and Peltier, ref. 3, p. 258. Return to text.
- Woodward, J., The Ice Age: A very short introduction, Oxford University Press, Oxford, p. 97, 2014. Return to text.
- Prell, W.L., Imbrie, J., Martinson, D.G. et al., Graphic correlation of oxygen isotope stratigraphy application to the late Quaternary, Paleoceanography 1(2):137–162, 1986. Return to text.
- Tauxe, L., Herbert, T., Shackleton, N.J., and Kok, Y.S., Astronomical calibration of the Matuyama-Brunhes boundary: consequences for magnetic remanence acquisition in marine carbonates and the Asian loess sequences, Earth and Planetary Science Letters 140:133–146, 1996. Return to text.
- Raymo, ref. 16, p. 578. Return to text.
- agupubs.onlinelibrary.wiley.com/doi/epdf/10.1029/97PA01169 Return to text.
- Tauxe, L., Deino, A.D., Behrensmeyer, A.K., and Potts, R., Pinning down the Brunhes/Matuyama and upper Jaramillo boundaries: a reconciliation of orbital and isotopic time scales, Earth and Planetary Science Letters 109:561–572, 1992. Return to text.
- Spell, T.L. and McDougall, I., Revisions to the age of the Brunhes-Matuyama boundary and the Pleistocene geomagnetic polarity timescale, Geophysical Research Letters 19(12):1181–1184, 1992. Return to text.
- Baksi, A.K., Hsu, V., McWilliams, M.O., and Farrar, E., 40Ar/39Ar dating of the Brunhes-Matuyama geomagnetic field reversal, Science 256(5055):356–357, 1992. Return to text.
- Mankinen, E.A. and Dalrymple, G.B., Revised geomagnetic polarity time scale for the interval 0-5 m.y. B.P., J. Geophysical Research 84(B2):615–626, 1979. Return to text.
- Hilgen, F.J., Astronomical calibration of Gauss to Matuyama Sapropels in the Mediterranean and implication for the geomagnetic polarity time scale, Earth and Planetary Science Letters 104(2–4):226–244, 1991. Return to text.
- Blaauw, M., Out of tune: the dangers of aligning proxy archives, Quaternary Science Reviews 36:38–49, 2010. Return to text.
- Blaauw, M., Bennett, K.D., and Christen., J.A., Random walk simulations of fossil proxy data, The Holocene 20(4):645–649, 2010. Return to text.
- Herbert, T.D., Paleoceanography: orbitally tuned timescales; in: Steele, J.H. (Ed.), Climates and Oceans, Academic Press, Amsterdam, The Netherlands, p. 374, 2010. Return to text.
- Raymo, ref. 16, p. 577. Return to text.
- Imbrie, J., Hays, J.D., Martinson, D.G. et al., The orbital theory of Pleistocene climate: support from a revised chronology of the marine d18O record; in: Berger, A., Imbrie, J., Hays, J., Kukla, G., and Saltzman, B. (Eds.), Milankovitch and Climate, part 1, D. Reidel Publishing, Dordrecht, Holland, pp. 269–305, 1984. Return to text.
- Martinson, D.G., Pisias, N.G., Hays, J.D., Imbrie, J.D., Moore, T.C., and Shackleton, N., (Table 2) SPECMAP stack of stable oxygen isotopes covering the last 300,000 years, PANGAEA, | doi.pangaea.de/10.1594/PANGAEA.56039?format=html#download. Supplement to Martinson et al., Age dating and the orbital theory of the ice ages: development of a high-resolution 0 to 300,000-year chronostratigraphy, Quaternary Research 27:1–29, 1987. Return to text.




Readers’ comments
Comments are automatically closed 14 days after publication.