Journal of Creation 26(3):101–106, December 2012
Browse our latest digital issue Subscribe
Information Theory—part 1: overview of key ideas
The origin of information in nature cannot be explained if matter and energy is all there is. But the many, and often contradictory, meanings of information confound a clear analysis of why this is so. In this, the first of a four-part series, the key views about information theory by leading thinkers in the creation/evolution controversy are presented. In part 2, attention is drawn to various difficulties in the existing paradigms in use. Part 3 introduces the notion of replacing Information by Coded Information System (CIS) to resolve many difficulties. Part 4 completes the theoretical backbone of CIS theory, showing how various conceptual frameworks can be integrated into this comprehensive model. The intention is to focus the discussion in the future on whether CISs can arise naturalistically.

Intelligent beings design tools to help solve problems. These tools can be physical or intellectual, and can be used and reused to solve classes of problems.1 But creating separate tools for each kind of problem is usually inefficient. In nature many problems involving growth, reproduction and adjustment to changes are performed with information-based tools. These share the remarkable property that an almost endless range of intentions can be communicated via coded messages using the same sending, transmission and receiving equipment.
All known life depends on information. But what is information and can it arise naturally? Naturalists deny the existence of anything beyond matter, energy, laws of nature and chance. But then where do will, choice, and information come from?
In the creation science and intelligent design literature we find inconsistent or imprecise understandings about what is meant by ‘information’. We sometimes read that nature cannot create information. But in other places, that some, but not enough, information could be produced to explain the large amount observed today in nature.
Suppose a species of bacteria can produce five similar variants of a protein which don’t work very well for some function, and another otherwise identical species produces only a single, highly tuned version. Which has more information?
Consider a species of birds with white and grey members. A catastrophe occurs and the few survivors only produce white offspring from now on. Has information increased or decreased?
What about enzymes. Do they possess more information when able to act on several different substrates or when specific to only one?
The influence of Shannon’s Theory of Information
Most of the experts debating the origin of information rely on the mathematical model of communication developed by the late Claude Shannon with its quantitative merits.2–4 Shannon’s fame began with publication of his master’s thesis, which was called “possibly the most important, and also the most famous, master’s thesis of the century”.5
Messages are strings of symbols, like ‘10011101’, ‘ACCTGGTCAA’, and ‘go away’. All messages are composed of symbols taken from a coding alphabet. The English alphabet uses 26 symbols, the DNA code, four, and binary codes use two symbols.
In Shannon’s model, one bit of information communicates a decision between two equiprobable choices and in general n bits between 2n equiprobable choices. Each symbol in an alphabet of s alternatives can provide log2s bits of information.
Entropy, H, plays an important role in Shannon’s work. The entropy of a Source can be calculated by observing the frequency each symbol i is generated in messages:

where log is to the base 2 and p is the probability of each symbol i appearing in a message. For example, if both symbols of an alphabet [0,1] are equiprobable, then eqn. (1) leads to:
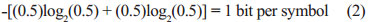
Maximum entropy results when the symbols are equiprobable, whereas zero entropy indicates that the same message is always produced. Maximum entropy indicates that we have no way of guessing which sequence of symbols will be produced. In English, letter frequencies differ, so entropy is not maximum. Even without understanding English, one can know that many messages will not be produced, such as sentences over a hundred letters long using only the letters z and q.6
Equations for other kinds of entropy, each with special applications, exist in Shannon’s theory: joint entropy, conditional entropy (equivocation), and mutual information.
Shannon devotes much attention to calculating the Channel Capacity. This is the rate at which the initial message can be transmitted error-free in the presence of disturbing noise, and requires knowledge of the probability that each symbol i sent will arrive correctly or be corrupted into another symbol, j. These error-correction measures require special codes to be devised, with additional data accompanying the original message.
There are many applications of Shannon’s theories, especially in data storage and transmission.7 A more compact code could exist whenever the entropy of the messages is not maximum, and the theoretical limit to data compression obtained by recoding can be calculated.8 Specifically, if messages based on some alphabet are to be stored or transmitted and the frequency of each symbol is known, then the upper compression limit for a new code can be known.9
Hubert Yockey is a pioneer in applying Shannon’s theory to biology.10–14 His work and the mathematical calculations have been discussed in this journal.15 Once it was realized that the genetic code uses four nucleobases, abbreviated A, C, G, and T, in combinations of three to code for amino acids, the relevance of Information Theory became quickly apparent. Yockey used the mathematical formalism of Shannon’s work to evaluate the information of cytochrome c proteins,15 selected due to the large number of sequence examples available. Many proteins are several times larger, or show far less tolerance to variability, as is the case of another example Yockey discusses:
“The pea histone H3 and the chicken histone H3 differ at only three sites, showing almost no change in evolution since the common ancestor. Therefore histones have 122 invariant sites … the information content of an invariant site is 4.139 bits, so the information content of the histones is approximately 4.139 × 122, or 505 bits required just for the invariant sites to determine the histone molecule.”16
Yockey seems to believe the information was front-loaded on to DNA about four billion years ago in some primitive organism. This viewpoint is not elaborated on by him and is deduced primarily by his comments that Shannon’s Channel Capacity Theorem ensures transmission of the original message correctly.
It is unfortunate that the mysterious allusions17 to the Channel Capacity Theorem were not explained. In one part he wrote,
“But once life has appeared, Shannon’s Channel Capacity Theorem (Section 5.3) assures us that genetic messages will not fade away and can indeed survive for 3.85 billion years without assistance from an Intelligent Designer.”18
This is nonsense. The Channel Capacity Theorem only claims that it is theoretically possible to devise a code with enough redundancy and error-correction to transmit a message error-free. Increased redundancies (themselves subject to corruption) are needed as the demand for accuracy increases, and perfect accuracy is achieved only at the limit of infinite low effective transmission of the intended error-free message. Whether this is even conceivable using mechanical or biological components is not addressed by the Channel Capacity Theorem. But the key point is that Yockey claims the theorem assures that the evolutionary message will not fade away. He confuses a mathematical ‘in principle’ notion with an implemented fact. He fails to show what the necessary error-correcting coding measures would be and that they have been actually implemented.
In his latest edition, Yockey (or possibly an editor) was very hostile to the notion of an intelligent designer. Tragically, his comments on topics like Behe’s irreducible complexity suggests he does not understand what the term means. As one example, we read:
“mRNA acts like the reading head on a Turing machine that moves along the DNA sequence to read off the genetic message to the proteasome. The fact the sequence has been read shows that it is not ‘irreducibly complex’ nor random. By the same token, Behe’s mouse trap is not ‘irreducibly complex’ or random.”19
Yockey’s work is often difficult to follow. Calculations which are easily understood and can be performed effortlessly with a spreadsheet or computer program are needlessly complicated by deriving poorly explained alternative formulations.20 Very problematic in his work is the difficulty in understanding his multiple uses of the word information. For example, the entropy of iso-1-cytochrome c sequences is called Information content.21 Then presumably the greater the randomness of these sequences, the higher the entropy and therefore the higher the information content, right? That makes no sense, and is the wrong conclusion. But why, since higher entropy of the Source (DNA) according to Shannon’s theory always indicates more information?
I believe this is the source of much confusion in the creationist and Intelligent Design literature which criticizes Shannon’s approach as supposedly implying greater randomness always implies more information.
Kirk Durston, a member of the Intelligent Design community, improves considerably on Yockey’s pioneering efforts. He correctly identifies the difference in entropy of all messages generated by a Source, H0, and the entropy of those messages which provide a particular function, Hf, as the measure of interest. He calls this difference, H0–Hf, functional information.22 This difference in entropies is actually used by all those applying Shannon’s work to biological sequences, whether evolutionists or not, although this fact is not immediately apparent when reading their papers.
Entropies are defined by eqn. (1), but Yockey’s approach has a conceptual flaw (and implied assumption) which destroys his justification for using Shannon’s Information Theory with protein sequence analysis.23 Truman already pointed out that Yockey’s quantitative results are obtained within little more than a rounding-off error with the same data, using much simpler standard probability calculations.24
The sum of the entropy contributions at each position of a protein leads to Hf. To calculate these site entropies, Durston aligned all known primary sequences of a protein using the ClustalX program, and determined the proportion of each amino acid in the dataset, using eqn. (1). Large datasets were collected for 35 protein families and the bits of functional information, or Fits, were calculated. Twelve examples were found having over 500 Fits, or a proportion of <2˗500 = 3 × 10˗151 among random sequences. The highest value reported was for protein Flu PB2, with 2416 Fits.
Durston’s calculations have one minor and one major weakness. To calculate H0, he assumed amino acids are equiprobable, which is not true. This effect is not very significant, but indeed H0 is a little less random than he assumed. The other assumption is that of mutational context independence: that all mutations which are tolerated individually are also acceptable concurrently. This is not the case, as Durston knows, and the result is that the amount of entropy in Hf is much lower than he calculated.15,25,26 The conclusion is that the protein families actually contain far more Fits of functional information, and represent a much lower subset among random sequences. This effect is counteracted somewhat by the fact that not all organisms which ever lived are represented in the dataset.
Bio-physicist Lee Spetner, Ph.D. from MIT, is a leading information theoretician who wrote the book Not by Chance.27 He is a very lucid participant in Internet debates on evolution and information theory, and is adamant that evolutionary processes quantitatively won’t increase information. In his book, he wrote,
“I don’t say it’s impossible for a mutation to add a little information. It’s just highly improbable on theoretical grounds. But in all the reading I’ve done in the life-sciences literature, I’ve never found a mutation that added information. The NDT says not only that such mutations must occur, they must also be probable enough for a long sequence of them to lead to macroevolution.”28
Within Shannon’s framework, it is correct that a random mutation could increase information content. However, one must not automatically conflate ‘more information content’ with good or useful.29,30
Although Spetner says information could be in principle created or increased, Dr Werner Gitt, retired Director and Professor at the German Federal Institute of Physics and Technology, denies this:
“Theorem 23: There is no known natural law through which matter can give rise to information, neither is any physical process or material phenomenon known that can do this.”31
In his latest book, Gitt refines and explains his conclusions from a lifetime of research on information and its inseparable reliance on an intelligent source.32 There are various manifestations of information: for example, the spider’s web; the diffraction pattern of butterfly wings; development of embryos; and an organ-playing robot.33 He introduces the term ‘Universal Information’34 to minimize confusion with other usages of the word information:
“Universal Information (UI) is a symbolically encoded, abstractly represented message conveying the expected actions(s) and the intended purposes(s). In this context, ‘message’ is meant to include instructions for carrying out a specific task or eliciting a specific response [emphasis added].”35
Information must be encoded on a series of symbols which satisfy three Necessary Conditions (NC). These are conclusions, based on observation.
NC1: A set of abstract symbols is required.
NC2: The sequence of abstract symbols must be irregular.
NC3: The symbols must be presented in a recognizable form, such as rows, columns, circles, spirals and so on.
Gitt also concludes that UI is embedded in a five-level hierarchy with each level building upon the lower one:
- statistics (signal, number of symbols)
- cosyntics (set of symbols, grammar)
- semantics (meaning)
- pragmatics (action)
- apobetics (purpose, result).
Gitt believes information is guided by immutable Scientific Laws of Information (SLIs).36,37 Unless shown to be wrong, they deny a naturalist origin for information, and they are:38
SLI-1: Information is a non-material entity.
SLI-2: A material entity cannot create a non-material entity.
SLI-3: UI cannot be created by purely random processes.
SLI-4: UI can only be created by an intelligent sender.
SLI-4a: A code system requires an intelligent sender.
SLI-4b: No new UI without an intelligent sender.
SLI-4c: All senders that create UI have a non-material component.
SLI-4d: Every UI transmission chain can be traced back to an original intelligent sender
SLI-4e: Allocating meanings to, and determining meanings from, sequences of symbols are intellectual processes.
SLI-5: The pragmatic attribute of UI requires a machine.
SLI-5a: UI and creative power are required for the design and construction of all machines.
SLI-5b: A functioning machine means that UI is affecting the material domain.
SLI-5c: Machines operate exclusively within the physical– chemical laws of matter.
SLI-5d: Machines cause matter to function in specific ways.
SLI-6: Existing UI is never increased over time by purely physical, chemical processes.
These laws are inconsistent with the assumption stated by Nobel Prize winner and origin-of-life specialist Manfred Eigen: “The logic of life has its origin in physics and chemistry.”39 The issue of information, the basis of genetics and morphology, has simply been ignored. On the other hand, Norbert Wiener, a leading pioneer in information theory, understood clearly that, “Information is information, neither matter nor energy. Any materialism that disregards this will not live to see another day.”40
It is apparent that Gitt views Shannon’s model as inadequate to handle most aspects of information, and that he means something entirely different by the word ‘information’.
Arch-atheist Richard Dawkins reveals a Shannon orientation to what information means when he wrote, “Information, in the technical sense, is surprise value, measured as the inverse of expected probability.”41 He adds, “It is a theory which has long held a fascination for me, and I have used it in several of my research papers over the years.” And more specifically,
“The technical definition of ‘information’ was introduced by the American engineer Claude Shannon in 1948. An employee of the Bell Telephone Company, Shannon was concerned to measure information as an economic commodity.”42
“DNA carries information in a very computer-like way, and we can measure the genome’s capacity in bits too, if we wish. DNA doesn’t use a binary code, but a quaternary one. Whereas the unit of information in the computer is a 1 or a 0, the unit in DNA can be T, A, C or G. If I tell you that a particular location in a DNA sequence is a T, how much information is conveyed from me to you? Begin by measuring the prior uncertainty. How many possibilities are open before the message ‘T’ arrives? Four. How many possibilities remain after it has arrived? One. So you might think the information transferred is four bits, but actually it is two.”40
In articles and discussions among non-specialists, questions are raised such as “Where does the information come from to create wings?” There is an intuition among most of us that adding biological novelty requires information, and more features implies more information. I suspect this is what lies behind claims that evolutionary processes cannot create information, meaning complex new biological features. Even Dawkins subscribes to this intuitive notion of information:
“Imagine writing a book describing the lobster. Now write another book describing the millipede down to the same level of detail. Divide the word-count in one book by the word-count in the other, and you have an approximate estimate of the relative information content of lobster and millipede.”40
Stephen C. Meyer, director of the Discovery Institute’s Center for Science and Culture and active member of the Intelligent Design movement, relies on Shannon’s theory for his critiques on naturalism.43,44 He recognizes that some sequences of characters serve a deliberate and useful purpose. Meyer says the messages with this property exhibit specified complexity, or specified information.45 Shannon’s Theory of Communication itself has no need to address the question of usefulness, value, or meaning of transmitted messages. In fact, he later avoided the word information. His concern was how to transmit messages error-free. But Meyer points out that
“… molecular biologists beginning with Francis Crick have equated biological information not only with improbability (or complexity), but also with ‘specificity’, where ‘specificity’ or ‘specified’ has meant ‘necessary to function’.”46
I believe Meyer’s definition of information corresponds to Durston’s Functional Information.
William Dembski, another prominent figure in the Intelligent Design movement, is a major leader in the analysis of the properties and calculations of information, and will be referred to in the next parts to this series. He has not reported any analysis of his own on protein or gene sequences, but also accepts that H0–Hf is the relevant measure from Shannon’s work to quantify information.
In part 2 of this series I’ll show that many things are implied in Shannon’s theory that indicate an underlying active intelligence.
Thomas Schneider is a Research Biologist at the National Institutes of Health. His Ph.D. thesis in 1984 was on applying Shannon’s Information Theory to DNA and RNA binding sites and he has continued this work ever since and published extensively.17,47
Senders and receivers in information theories
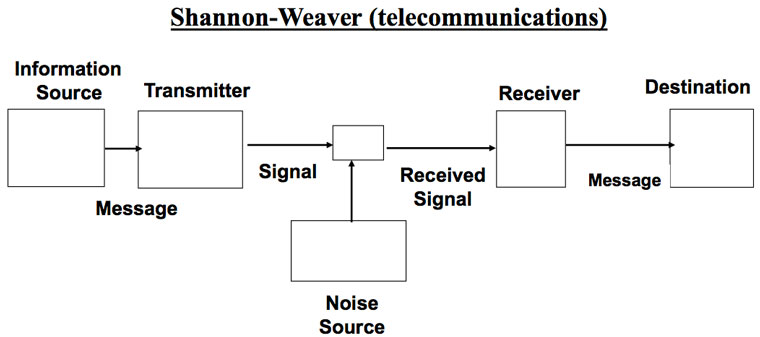
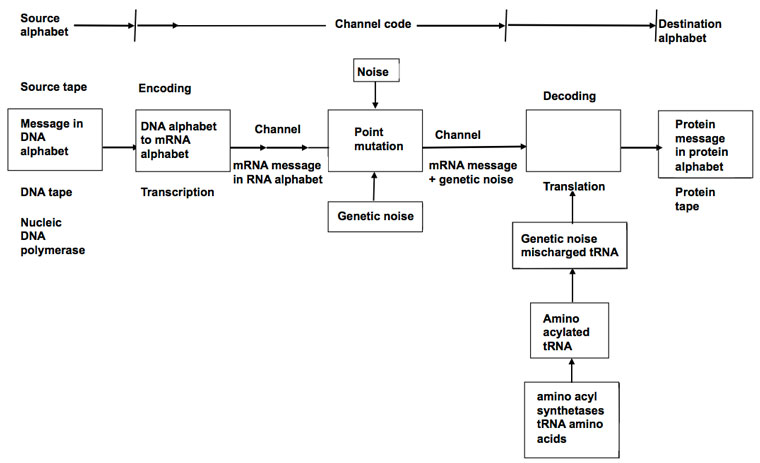
There is common agreement that a sender initiates transmission of a coded message which is received and decoded by a receiver. Figure 1 shows how Shannon depicted this and figure 2 shows Yockey’s version.2,17

A fundamental difference in Gitt’s model is the statement that all levels of information, including the Apobetics (intended purpose) are present in the Sender (figure 3). All other models treat the Sender as merely whatever releases the coded message to a receiver. In Shannon’s case, the Sender is the mindless equipment which initiates transmission to a channel. For Yockey the Sender is DNA, although he considers the ultimate origin of the DNA sequences open. Gitt distinguishes between the original and the intermediate Sender.48
Humans intuitively develop coded information systems
Humans interact with coded messages with such phenomenal skill, most don’t even notice what is going on. We discuss verbally with ease. Engineers effortlessly devise various designs: sometimes many copies of machines are built and equipped with message-based processing resources (operating systems, drivers, microchips, etc.). Alternatively, the hardware alone could be distributed and all the processing power provided centrally (such as the ‘dumb terminals’ used before personal computers). To illustrate, intellectual tools such as reading, grammar, and language can be taught to many students in advance. Later it is only necessary to distribute text to the multiple human processors.
The strategy of distributing autonomous processing copies is common in nature. Seeds and bacterial colonies already contain preloaded messages, ribosomes already possess engineered processing parts, and so on.
Conclusion
The word information is used in many ways, which complicates the discussion as to its origin. The analysis shows two families of approaches. One is derived from Shannon’s work and the other is Gitt’s. To a large extent the former addresses the how question: how to measure and quantify information. The latter deals more with the why issue: why is information there, what is it good for?
The algorithmic definition of information, developed by Solomonoff and Kolmogorov, with contributions from Chaitin, is rarely used in the debate about origins and in general discussions about information currently. For this reason it was not discussed in this part of the series.
References and notes
- A physical tool, such as a saw can be used to cut various kinds of material. Intellectual tools, like regression analysis, Bayes’ theorem, and probability theory, can be used to solve a wide range of problems in different domains. Return to text.
- Shannon, C.E., A mathematical theory of communication, Bell System Technical J. 1948, (July, October), pp. 379–423, 623–656; cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf. Return to text.
- Shannon, C.E. and Weaver, W., The Mathematical Theory of Communication, University of Illinois Press, IL, 1998. Return to text.
- I’ve had personal correspondence with all the experts mentioned in this paper except Dawkins, and therefore know their viewpoints. Return to text.
- Horgan, J., Unicyclist, juggler and father of information theory, Scientific American 262:22–22B, 1990. Return to text.
- The probabilities of these letters appearing in random sentences are: z = 0.074 and q = 0.095, en.wikipedia.org/wiki/Letter_frequency. Return to text.
- en.wikipedia.org/wiki/Shannon_information_theory. Return to text.
- Togneri, R. and deSilva, C.J.S., Fundamentals of Information Theory and Coding Design, Taylor & Francis Group, Boca Raton, FL, 2003. Return to text.
- Truman, R., An evaluation of codes more compact than the natural genetic code, J. Creation 26(2):88–99, 2012. Return to text.
- Yockey, H.P., Information Theory And Molecular Biology, Cambridge University Press, Cambridge, UK, 1992. Return to text.
- Yockey, H.P., On the information content of cytochrome c, J. Theor. Biol. 67(3):345 –396, 1977. Return to text.
- Yockey, H.P., A prescription which predicts functionally equivalent residues at given sites in protein sequences, J. Theor. Biol. 67(3):337–343, 1977. Return to text.
- Yockey, H.P., An application of information theory to the central dogma and the sequence hypothesis, J. Theor. Biol. 46(2):369–406, 1974. Return to text.
- Yockey, H.P., Origin of life on earth and Shannon’s theory of communication, Computers & Chemistry 24(1):105–123, 2000. Return to text.
- Truman, R. and Heisig, M., Protein families: chance or design? J. Creation 15(3):115–127, 2001. Return to text.
- Yockey, ref. 10, p. 244. Return to text.
- Yockey, H.P., Information Theory, Evolution, and the Origin of Life, Cambridge University Press, MA, 2005. Return to text.
- Yockey, ref. 17 p. 181. Return to text.
- Yockey, ref. 17 p. 181. See also p. 179 for a similar statement. Return to text.
- Yockey, ref. 17, chapter 5 contains the substance of Yockey’s calculations. The ‘simplifications’ in pp. 49–56 only confuse and seem to have led to multiple errors in table 5.2. Since I have communicated other errors to him in the past, this leads to doubts as to whether one has understood correctly, being unable to reproduce the results claimed. Return to text.
- Yockey, ref. 17, p. 59, tables 6.3 and 6.5. Return to text.
- Durston, K., Chiu, D.K.Y., Abel, D.L. and Trevors, J.T., Measuring the functional sequence complexity of proteins, Theoretical Biology and Medical Modelling 4(47):1–14, 2007; www.tbiomed.com/content/4/1/47/. Return to text.
- This is discussed in Appendix 1, creation.com/information-theory-part-1#1. Return to text.
- Truman, R. and Heisig, M., Protein families: chance or design? J. Creation (formerly TJ) 15(3):115–127, 2001. Return to text.
- Truman, R., Protein mutational context dependence: a challenge to neo-Darwinian theory: part 1, J. Creation (formerly TJ) 17(1):117–127, 2003. Return to text.
- Personal communications with Kirk Durston. He is working on another formulism which takes joint probabilities into account. Return to text.
- Spetner, L., Not by Chance! Shattering the Modern Theory of Evolution, The Judaica Press, Brooklyn, New York, 1998. Return to text.
- Spetner, ref. 27, pp. 131–132. Return to text.
- For example, better immune protection results if a wider variety of chemical environments, generated by a combination of different amino acids, are available at the epitome binding site of B cell receptors, to help identify more protein antigens coming from unwanted bacterial or viral invaders. Greater variety implies lower information content. However, once an antigen has been bound, guided mutations can fine-tune the nature of the epitome binding site to permit finding other invader cells which possess foreign proteins (from which the protein antigen came). Now the narrower variety of epitome-binding sites represent an information increase. Return to text.
- Further information on Spetner’s work is provided in Appendix 2, creation.com/information-theory-part-1. Return to text.
- Gitt, W., In the Beginning was Information, CLV, Bielenfeld, Germany, p. 79, 1997. Return to text.
- Gitt, W., Compton, B. and Fernandez, J., Without Excuse, Creation Book Publishers, 2011. Return to text.
- Gitt, ref. 31, chapter 1. Return to text.
- Gitt, ref. 32, chapter 2. Return to text.
- Gitt, ref. 32, p. 70. Return to text.
- Gitt, W., Scientific laws of information and their implications part 1, J. Creation 23(2):96–102, 2009; creation.com/laws-of-information-1. Return to text.
- Gitt, W., Implications of the scientific laws of information part 2, J. Creation 23(2):103–109, 2009; creation.com/laws-of-information-2. Return to text.
- Gitt, ref. 32, chapter 5. Return to text.
- Eigen, M., Stufen zum Leben—Die frühe Evolution im Visier der Molekularbiologie, Piper-Verlag, München, p. 149, 1987. Return to text.
- Wiener, W., Cybernetics or Control and Communication in the Animal and the Machine, Hermann et Cie., The Technology Press, Paris, 1948. Return to text.
- Dawkins, R., Unweaving the Rainbow, Houghton Mifflin, New York, p. 259, 1998. Return to text.
- Dawkins, R., The Information Challenge, www.skeptics.com.au/publications/articles/the-information-challenge/, Accessed 5 February 2012. Return to text.
- Meyer, S., The origin of biological information and the higher taxonomic categories, Proc. Biol. Soc. 117(2):213–239, 2004. Return to text.
- Meyer, S., Signature in the Cell: DNA and the Evidence for Intelligent Design, HarperOne, New York, 2009. See especially chapter 4. Return to text.
- Meyer, ref. 44, p. 107. Return to text.
- Meyer, ref. 44, p. 109. Return to text.
- Thomas Schneider’s work is outlined in Appendix 3, creation.com/information-theory-part-1. Return to text.
- Gitt, ref. 36, p. 100. Return to text.



Readers’ comments
Comments are automatically closed 14 days after publication.