Journal of Creation 28(2):6–8, August 2014
Browse our latest digital issue Subscribe
Organized complexity—how atheistic assumptions hinder science

One of evolution’s outstanding problems is the origin of information. How can it be that biological systems which can express apparent purpose (in teleological terms) have arisen through completely natural processes? Heedless to the consequences to their own arguments, evolutionists have long argued that purpose is an illusion. The line of argument is simple:
- Order is mistaken for purpose.
- Order is a result of natural processes.
- Hence what appears to be purpose is actually a result of natural processes.
The latest turn at making this argument falls to complexity theory, on the basis of which Melanie Mitchell argues:
“Most biologists, heritors of the Darwinian tradition, suppose that the order of ontogeny is due to the grinding away of a molecular Rube Goldberg machine, slapped together piece by piece by evolution. I present a countering thesis: most of the beautiful order seen in ontogeny is spontaneous, a natural expression of the stunning self-organization that abounds in very complex regulatory networks. We appear to have been profoundly wrong. Order, vast and generative, arises naturally.”1
Again, however, this argument is taken forward heedless of the results of its actual outcome. What is the actual outcome of the argument from complexity theory? First, equating complexity with purpose defeats itself in demoting the thinking required to reach the conclusion offered from purposeful thought to simply ordered thought without meaning. Second, equating complexity with purpose closes off any hope of explaining and understanding ordered, or designed, complexity. It is this second result this article examines in some detail.
Ordered complexity
Complexity is, as complexity theorists would like to say (in an ironic turn of phrase), an emergent field of study. From corporate financials, to the stock market, to social networking, complexity is on the cutting edge of current research—and with good reason. In each of these areas, researchers and engineers are discovering and rediscovering many of the same principles and ideas, finally bumping up against one another’s writing and finding parallel strains across fields as diverse as computer networking and biology.
Standing across the path in all these fields is a single obstacle: ordered complexity. As Weaver explained the problem in 1948:
“This new method of dealing with disorganized complexity, so powerful an advance over the earlier two-variable methods, leaves a great field untouched. One is tempted to oversimplify, and say that scientific methodology went from one extreme to the other—from two variables to an astronomical number—and left untouched a great middle region. The importance of this middle region, moreover, does not depend primarily on the fact that the number of variables involved is moderate—large compared to two, but small compared to the number of atoms in a pinch of salt. The problems in this middle region, in fact, will often involve a considerable number of variables. The really important characteristic of the problems of this middle region, which science has as yet little explored or conquered, lies in the fact that these problems, as contrasted with the disorganized situations with which statistics can cope, show the essential feature of organization. In fact, one can refer to this group of problems as those of organized complexity.”2
As an example of disordered complexity, Weaver offers a pool table with no side pockets (hence no place for the balls to exit the table), a perfectly frictionless surface, and perfectly rebounding bumpers (figure 1). Place on this table ten balls that can strike one another without losing energy—in short, suspend the laws of thermodynamics for this table and these balls. Now start the ten balls moving in random directions.
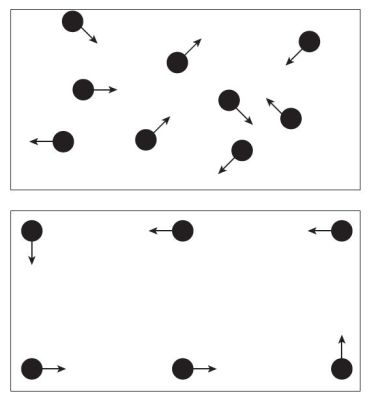
Fairly simple math can be used to predict the movement of each ball in some detail, including its impact with the bumpers and other balls. At any given moment, knowing the origin, energy, and direction of each ball at the moment all this movement starts, it’s possible to calculate the position and direction of travel of any given ball at any other moment in time. Take away all knowledge of the original location, direction, and amount of energy and simply observe the balls as they move about the table. More complex math, developed in the last few decades, can still predict the probability of any given ball being at any particular point on the table at any point in time. Statistics have come a long way in the area of unordered complexity.
But place the balls so they are all perfectly aligned and set them in motion so each ball will move around the table without touching another ball, and the math ceases to explain (figure 1). The path of each ball can be independently calculated but there is no way to describe the system as a whole. This is ordered complexity. It’s easy to extend the example with ordered interactions; a perfectly designed system can cause the balls to interact in a way that allows the observer to always know where any given ball will be and what the pattern of interaction will be into the indeterminate future. Even in this situation, the observer will not be able to determine how the system came to be in this state, only predict what the interactions will be among the various balls. Nor can the system be described as a system, rather as individual pieces. While a single formula or set of formulas can be used to describe a disordered system, an ordered system requires a set of formulas.
Weaver placed great weight on the shoulders of the study of organized complexity, from the price of wheat to the stability of currency. Like Weaver, the modern social engineer is placing the same weight on the shoulders of organized complexity. Data scientists, biologists, and those who would build a utopia rely on solving the organized complexity puzzle.
Possible solutions to ordered complexity
So where are we now? What new progress has been made in understanding organized complexity? There are at least two specific recent attempts to explain ordered complexity and its existence in the world around us.3
Relational order theory is the current trend in thinking around complexity. In relational order theory, the position and characteristics of any particular object is only meaningful in relation to other objects. Thus an atom only exists in any meaningful way in relationship to other atoms and space does not exist except in relation to the objects within that space. Processes, in a sense, are embedded into the physical world.4
But this just begs the fundamental question that organized complexity presents: where did the organization come from?
To say that it is just a part of nature is to essentially say nothing at all. Assuming that order is an inherent part of the physical world, and that this inherent order somehow ‘emerges’ from within the physical world as a matter of course, doesn’t answer the question of how order became a part of the physical world. Making these assumptions doesn’t help to explain ordered complexity as a system. It simply posits an alternate source of order other than a designer.
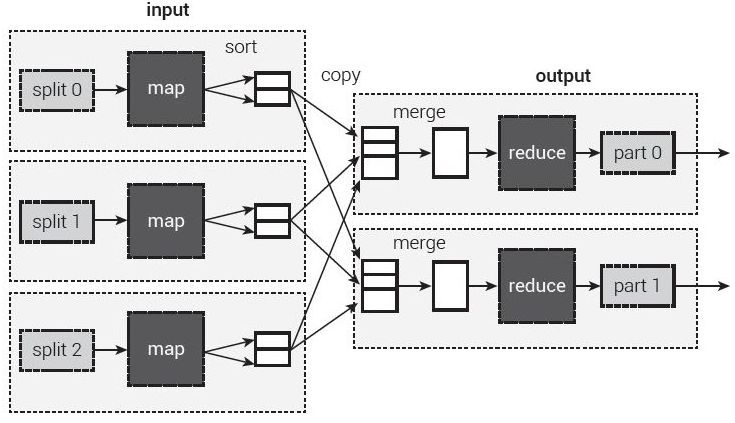
Another effort worth noting is big data analytics. Pioneered by Google, the map/reduce paradigm illustrated in figure 2 is used to find patterns in large scale data sets. Big data is sometimes touted as the solution to understanding, and even managing, societal behaviour. According to Alex Pentland, a pioneer in big data:
“Understanding these human-machine systems is what’s going to make our future social systems stable and safe. We are getting beyond complexity, data science and web science, because we are including people as a key part of these systems. That’s the promise of Big Data, to really understand the systems that make our technological society. As you begin to understand them, then you can build systems that are better. The promise is for financial systems that don’t melt down, governments that don’t get mired in inaction, health systems that actually work, and so on, and so forth.”5
But big data faces a big problem: it doesn’t always work. Peering deep into the recesses of the big data and its assumptions can uncover two reasons for this problem. First, big data analysis assumes that all the right variables have been collected and pushed into the right algorithm to find the right trend at the right time. That’s an awful lot of ‘rights’ piled on top of one another. Second, big data assumes emergent order and goes about trying to find it by throwing computational power at the problem. Big data, at its foundation, doesn’t try to explain ordered complexity. It simply assumes ordered complexity is a natural property of all complex systems and then sets about trying to discover that order.
But what if order isn’t really emergent in the way big data postulates? In this case, we can expect some early success, followed by a long unwinding, or a lull in progress denoting the trend has reached its peak. As an article in the Financial Times on the unwinding of big data notes, we should (and can) never assume we have all the data.6 Google Flu’s failure in actually predicting the location and extent of 2014’s flu season is an illustrative example pointed out in the article. Anecdotal stories of false positives abound in the real world but never seem to be addressed in ‘the literature’. The New York Times notes nine problems with big data, including, “[big data] never tells us which correlations are meaningful”, the risk of finding apparent correlations that really aren’t, and the echo-chamber effect.7 Big data turns on the concept that all complexity is ordered complexity; treating all complexity as ordered will lead to discoveries of order in apparently unordered data sets that results in the ability to predict (and hence control) the world, even if it is one person at a time. That big data fails should be an alert on the ordered complexity front.
No, we still don’t understand ordered complexity. Begging the question and assuming emergence simply aren’t going to solve the underlying problem, either. What is the problem, then?
At the root lies a materialistic assumption: all there is, is matter. If order exists, that order must come from the matter itself in some way. This is carried further in big data; if matter self-organizes, then people must also self-organize in much the same way. The actual existence of ordered complexity becomes proof that emergence must be real; self-organization is somehow ‘built into the DNA’ of the universe (although the universe actually has no DNA). As one atheist, Krauss, states:
“Every day beautiful and miraculous objects suddenly appear, from snowflakes on a cold winter morning to vibrant rainbows after a late-afternoon summer shower. Yet no one but the most ardent fundamentalists would suggest that each and every such object is lovingly and painstakingly and, most important, purposefully created by a divine intelligence. In fact, many laypeople as well as scientists revel in our ability to explain how snowflakes and rainbows can spontaneously appear, based on simple, elegant laws of physics.”8
Many mathematicians and scientists spend time trolling through complexity theories trying to explain design away simply because they can’t accept the existence of a designer. Perhaps, as Krauss believes, there is an answer in simply positing every possible universe that could ever exist has actually existed. On the other hand, a theory that explains every possible outcome has no final explanatory power.
Conclusion
We can’t solve the problems of ordered complexity using the tools of randomness; nor can we explain the order we find in nature by sweeping it under the ‘rug of emergence’. Instead, to make progress on the ordered complexity front, science must face design squarely. Atheism is blind to teleology; materialistic worldviews must reject any concept of purpose at the risk of letting the nose of God into the tent—but ordered complexity, at a systemic level, will ultimately only make sense in the context of teleology, or final intent.
By ignoring design—by assuming emergence—atheistic science is blind to design, and therefore cannot even begin to approach the problem of ordered complexity. This truly harms the progress of science by directing a lot of research time and money down blind alleyways, and by stopping science from asking that one all-important question: why?
References and notes
- Mitchell, M., Complexity: A Guided Tour, Oxford University Press, New York, p. 286, 2009. Return to text
- Weaver, W., Science and complexity, American Scientist 36(4):539, 1948 | jstor.org/stable/27826254. Return to text
- A realm of inquiry not covered here is the various attempts at finding a Grand Unified Theory (GUT) that will explain the interaction of all the various systems present in the universe by finding the relationship between the four forces. No widely accepted model of a GUT has emerged, however, and any model that does emerge will still face the problem of where the order on which the model rests comes from. Herrmann, for instance, has been working on a grand unification model that does, in fact, posit an underlying intelligence; see The GGU-model and the GID-model Processes and Their Secular and Theological Interpretations, vixra.org, accessed 18 April 2014. Return to text
- Relational Order Theories, en.wikipedia.org, accessed 12 April 2014. Return to text
- Pentland, A., Reinventing Society in the Wake of Big Data, edge.org, accessed April 2014. Return to text
- Harford, T., Big Data: Are We Making a Big Mistake?, Financial Times, 28 March 2014, ft.com, accessed April 2014. Return to text
- Marcus, G. and Davis, E., Eight (No, Nine!) Problems With Big Data, The New York Times, 6 April 2014, nytimes.com, accessed April 2014. Return to text
- Krauss, L.M., A Universe from Nothing: Why There is Something Rather than Nothing, Free Press, New York, p. xi, 2012. Return to text










Readers’ comments
Comments are automatically closed 14 days after publication.