Journal of Creation 25(3):109–111, December 2011
Browse our latest digital issue Subscribe
Does observational evidence indicate the universe is expanding?—part 1: the case for time dilation

In the late 1920s Hubble discovered what is now called the Hubble Law, relating the distance to the redshift of a galaxy, which is explained in terms of an expanding universe. This claim is reviewed in light of the lack of necessary evidence for time dilation in quasars and gamma-ray burst luminosity variations and other lines of evidence.
Ever since the late 1920s, when Edwin Hubble discovered a simple proportionality1 between the redshifts of the light coming from nearby galaxies and their distances, we have been told that the universe is expanding. This relationship—dubbed the Hubble Law—has since been strengthened and extended to very great distances in the cosmos. Nowadays it is considered to be the established dogma of the expanding big bang universe. This means that the space that contains the galaxies is expanding and that the galaxies are essentially stationary in that space, but being dragged apart as the universe expands.

Hubble initially interpreted his redshifts as a Doppler effect, due to the motion of the galaxies as they rushed away from our location in the universe. He called it a ‘Doppler effect’ as though the galaxies were moving ‘through space’—the space is not expanding, and that is how some people, especially astronomers, initially perceived it. This is different to what has now become accepted, but observations alone could not distinguish between the two concepts. Later in his life Hubble varied from his initial interpretation and said that the Hubble Law was due to a hitherto undiscovered mechanism, but not due to expansion of space—now called cosmological expansion.
The big bang expanding universe model essentially offers a coherent paradigm or explanatory framework which can, in principle, provide answers to a wide range of key cosmological questions; examples are the origin of extragalactic redshifts, the dynamical state of the universe (i.e. not apparently collapsing under gravity), Olbers’ paradox (why is the night sky dark?), the origin of the cosmic microwave background (CMB) radiation, the origin of galaxies, and the origin of the elements. The fact that its answers to some questions are currently unsatisfactory or unconvincing does not change the basic point that such a model will always be preferred to a more limited model such as a static Euclidean universe, which does not attempt to address such questions. In this sense the big bang model is necessarily preferable regardless of one’s theological position.
However, to date there is no experimental local laboratory evidence that establishes cosmological expansion as a real phenomenon of nature. Though it can be derived as a consequence of Einstein’s General Relativity Theory,2 it has been claimed by some as a fudge factor3 to prop up the ailing standard Lambda cold dark matter (ΛCDM) big bang model, also called the concordance model for the big bang origin and structure of the universe. This paper compares the evidence for and against the concept of cosmological expansion. It necessarily compares it to a static universe.
It must be stated at the outset that the Hubble Law can be derived from general relativity, with an appropriate choice of energy-momentum tensor and metric. And that general relativity has been successfully empirically tested in the solar system by numerous tests is a very strong point in its favour. But it does not prove it, and unless a physical mechanism can be established that produces a Hubble Law in static universe, then this fact favours the expanding universe. The question of stability against gravitational collapse also counts significantly in favour of the concordance model, which naturally includes the effect of gravity in its formulation. In a static Euclidean model one either has to postulate that collapse is occurring, but on a very long timescale, or postulate some other force field which counteracts gravity; neither would seem an especially attractive option.
The physical evidence
All evidence for cosmological expansion comes from the cosmos itself. Supernovae (exploding stars; see figure 1) are among the brightest light sources in the sky. Astrophysicists believe that they have successfully understood the origin of a certain class of these explosions using known physics, including general relativity theory, where a white dwarf star, after accumulating sufficient mass from a companion star to reach a critical limit, catastrophically explodes in a blinding flash of light. The luminosity of the explosion rapidly increases, peaks, and then slowly decreases over days and months. By modelling this, it is believed that one can understand what the intrinsic brightness at the peak of the explosion was, and hence one can establish, for a certain class of these supernovae, a ‘standard candle’. The theory says that the intrinsic brightness at the peak of the explosion is the same for all supernovae in this class—the type 1a, which are identified from the metal content in their spectra. This means if you know their intrinsic brightness you can determine their distance in the cosmos. Then using the redshifts of their host galaxies and the Hubble redshift-distance relation (see figure 2), the distance modulus, derived from the standard cosmology, the theory can be tested with the matter density (Ωm)4, the dark energy density (ΩΛ)5 and the Hubble constant (H0) as the only free parameters.
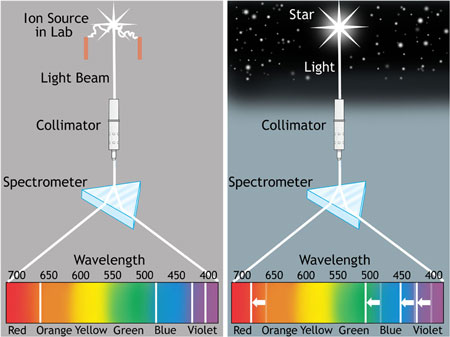
From this astronomers claim not only that the universe is expanding but also that the expansion is accelerating. In order to make their observations fit the standard cosmology, they have had to add dark energy with a non-zero value for the cosmological constant (Λ) and also a significant amount of dark matter.6 Together these comprise about 96% of the mass-energy content of the universe, yet they remain unknown entities. However, without them the ΛCDM big bang (BB) model seriously fails to describe the observed luminosities.
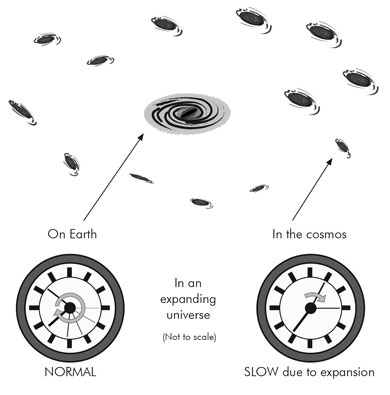
One of the consequences of cosmological expansion is time dilation. When the light curves, which show the rise and fall in luminosity of the supernova explosion, are compared at increasing redshifts, their time axes should be stretched due to time dilation with respect to the observer on Earth. In other words, processes that follow a flow of time in the distant cosmos are slowed relative to Earth time, i.e. when observed from Earth (see figure 3). This time dilation effect has been clearly observed in the light curves of this type of supernova and is claimed as definitive evidence for expansion.14 Yet, no time dilation has been observed in the luminosity variations of quasars,30,33 which are meant to be at very great distances based on their redshifts and the Hubble law. How can these contradictory claims be reconciled?
Add to this the evidence that some quasars are apparently associated with relatively low-redshift galaxies,7,8 which can only be reconciled if those quasars are not at their redshift distances but are located nearby. And the fact that proper motion (movement against background celestial objects during a year) is observed in quasars9 really brings into doubt that at least some of them must not be at the supposed cosmological distances based on their redshifts. That means that a large part of a quasar’s redshift must be due to some as-yet-unknown non-cosmological cause, i.e. not due to expansion of space. If verified, this is very damaging to the standard model.
Considering the history of the expanding universe hypothesis, the burden of proof should really rest with those that make the claim. Hubble first thought that the redshifts of the galaxies were due to a Doppler effect (motion of the galaxies through space) but as cosmology developed, some showed theoretically that the effect was due to the expansion of space over the period of flight of the photons from emitter to receiver. Hence it is called cosmological expansion. And the reality is it is claimed to be independent of the emitter source. If independent then that means the origin of the redshifts comes from a process during the flight of the photon from source to receiver. The expansion of space itself is currently the best argument for this.
The question must be asked, what physical evidence do we have that the universe is expanding? In 2003 López-Corredoira15 reviewed the evidence for this and other questions for cosmology today. This paper (in two parts) focuses on a review of some of those evidences.
Evidence for time dilation
Type 1a supernovae
The type 1a supernova (SN) measurements are the very best evidence for an expanding universe. In 1998 two independent projects (the Supernova Cosmology Project10 and the High-z Supernova Search11) announced not only was the universe expanding but also accelerating.12 They examined a certain class of supernova and studied the light curves—the brightening and subsequent decay of the light intensity of the explosions. The peak brightness or luminosity (L) they correlated to an absolute magnitude (MB ~ –2.5 log(L)), which is assumed to be an intrinsic brightness fundamental to the class of supernova.
The light curves were adjusted for a stretch factor w = s(1+z) which is claimed to be due to time dilation as a function of epoch (z), the redshift of the source. This is absolutely required in an expanding universe. In fact, it is the only redshift mechanism on offer that requires it. To my knowledge this time dilation factor is the only evidence for an expanding universe that sets it apart from a static universe. The Hubble Law—the relationship between the apparent magnitudes (hence distances from luminosities) and redshifts of galaxies—is not sufficient grounds to establish an expansion. Theoretically there are other possible redshift mechanisms and to date one author has compiled 31 mechanisms giving a quantitative description of how large redshifts may be related to distance.13
With the analysis of the supernova light curves, the correction—the stretch factor (w)—is determined by hand, an empirical fit to the best selected data. The study that showed the most constrained results found a sample of light curves proportional to (1+z)b where b = 1.07 ± 0.06.14 This seems to be the most definitive measurement of time dilation where b should be identical with unity. However, a possible criticism is that the time under the light curve could depend on the intrinsic brightness of the supernovae (i.e. the correction s), which might vary considerably with the redshift (z).15 Ref. 15 has a very good review of this. A similar point is made by Crawford,16
“Since current investigators assume that the type 1a supernovae have essentially a fixed absolute BB [the standard ΛCDM cosmology] magnitude (with possible corrections for the stretch factor), one of the criteria they used is to reject any candidate whose predicted absolute peak magnitude is outside a rather narrow range. The essential point is that the absolute magnitudes are calculated using BB and hence the selection of candidates is dependent on the BB luminosity-distance modulus [emphasis added].”
Basically he is claiming it is selection bias. This is circular reasoning; select only the candidates that fit the desired luminosity-distance criteria and use them to determine the luminosity distance. Since one cannot determine the absolute magnitudes of the sources without assuming a cosmology, the standard concordance criteria (Ωm ~ 0.3, ΩΛ ~ 0.7, and H0 ~ 70 km/s/Mpc) are used to calculate the absolute magnitudes for the candidates, which must be in a narrow range, near MB ~ –19, and the acceptable ones are used to test the same model, and therefore determine values for Ωm and ΩΛ. This is confirmed by Foley et al.23 who state,
“… for any individual SN 1a, the intrinsic width is unknown, so without assuming a (1+z) dilation, the intrinsic width and dilation cannot be separated.”
Nevertheless for the selected supernovae the regression fit to the derived absolute magnitudes (MB) of the sources on the expected 2.5 log(1 + z) redshift dependence shows that the luminosity is proportional to (1 + z)a, where a = 0.23 ± 0.07. This means that their intrinsic luminosity must have slowly decreased as the universe evolved.17 Note Fig. 13 (page 1036) of Reiss et al.18 where various SN 1a light curves are shown with different absolute magnitudes MB. The brighter sources decline slower than the dimmer sources. The standard explanation for this change is the ad hoc introduction of dark energy19 or quintessence.20 Hence evolution in the size and mass of the galaxies over cosmic time has been assumed as the reason. The question then remains what level of circular reasoning has been used from selection of the candidate type 1a supernovae (plural abbreviation: SNe 1a) because they do not (as initially assumed for a standard candle) have the same intrinsic luminosities?
Crawford16 models the luminosities of type 1a supernova in a static universe and finds that the total energy of the explosion (area under the light curve) is a far better ‘standard candle’. Therefore, assuming that all these types of supernovae have essentially the same energy, based on the modelling of the critical Chandrasekhar mass limit of the progenitor white dwarf, the product of the peak luminosity and the width of light curve will be a constant. Since the prime characteristic used for selecting these supernovae is the peak absolute magnitude, which is computed using the standard concordance model,21 there is a strong bias that results in intrinsically weaker supernovae being selected at higher redshifts. And for constant energy these weaker supernovae must have wider light curves. This is a selection effect that has the width of the light curve increasing with redshift and hence can mimic time dilation in the resulting selected candidates.
When Crawford16 applies his model of absolute energy (absolute magnitude in his static model plus correction for width) for each supernova in the same SN 1a data sets22 used by the BB community, he finds the energy of the explosion to be invariant over all redshifts with a curve-fit slope of 0.047 ± 0.089, which is consistent with zero. This means no change over all redshifts. Using a simple selection model for SN 1a data, he shows their width-dependence on redshift, and considering the biased nature of the data, it is a very reasonable fit. Hence no time dilation and no cosmological expansion. Because no additional energy is needed for the fit, no dark energy or quintessence is needed either.
In an effort to resolve this time dilation question in supernova light-curves a single supernova (1997ex) was studied23 at different epochs separated by months, and found that the spectral evolution of the source is inconsistent with no time dilation at a very high confidence level. The claim lies in the spectral-feature age that is used to independently determine the aging of the source at approximately monthly intervals. The derived age measure is then compared to the expected (1+z) aging. Hence the amount of aging in the supernova rest frame should be a factor of (1 + z)−1 smaller than that in the observer frame. The results were found to be consistent with time dilation. It should also be mentioned that this latter paper discusses the consistency of time dilation seen both in the SN light-curve, over monthly timescales, and in the wavelengths of the light seen in the observer frame, i.e. in the redshifting of the light from the source. This is the important distinction for this review. Are longer timescale time measures consistent with the “femtosecond time dilation” in the observed redshift of the light from the sources?
The concept of the accelerating universe has come from the very highest redshift type 1a supernova observations, and hence the idea of dark energy (or a cosmological constant) driving the universe apart. This has resulted from a deficit of the expected luminosity determined from the standard model with Λ = 0 and that observed in these distant sources. However it has also been criticized on the basis of intergalactic dust24,25 causing the added deficit and that the presence of grey dust is not inconsistent with the measure on the most distant supernova at redshift z = 1.7 (SN 1997ff).25
Type 1a supernovae may also have a metallicity26 dependence on redshift, which may mean that the resulting non-zero value of the cosmological constant may require corrections for metallicity by factors as large as the effects of the assumed cosmology itself.27 This causes an underestimate of the effects of host galaxy extinction; a factor which contributes to the apparent faintness of the high-redshift supernovae is evolution of the host galaxy extinction as a function of redshift, caused by the presence of gases (other than hydrogen and helium) and dust. Therefore with a proper treatment of the latter, and if one eliminates those SN 1a sources not observed before peak brightness is reached, the evidence for a cosmological constant (and dark energy) is quite weak.
Ivanov has developed a quantum gravity static universe model28 that has a Hubble Law resulting from quantum interactions. There is no time dilation in his model. The author compares the predictions of his model with both SNe 1a and GRBs without time dilation.29 In other words he corrects the published SN 1a distance modulii for the time dilation stretch factor and compares with his model. The fits are extremely good yet no dark energy term is needed. Ivanov concludes his paper with the telling remark,
“ … the discovery of dark energy in a frame of the standard cosmological model is only an artefact of the conjecture about an existence of time dilation.”
This confirms the circularity involved here. So one can say then that if there exists at least one static model where if one corrects the SN 1a data for no time dilation and it fits that model, then that creates significant doubt about the need for dark energy and dark matter in the first instance.
Quasar luminosity variations
As mentioned above no time dilation is found in quasar observations. This is powerful evidence against any time dilation effects in the universe as a function of epoch or expansion redshift (z).
Quasars show variations in their luminosities over timescales of weeks to years. Research by Hawkins from 1975 to 2002 provides very strong evidence that quasars do not exhibit any time dilation.30,33 His evidence covers timescales from 50 days to 28 years and uses Fourier power spectral analysis. Data from groups of quasars at low (z < 1) and high redshift (z > 1) are compared to look for changes expected from time dilation. They do not show any when considered from the observer’s frame of reference. How can this be reconciled with the SN 1a measurements? There is also an anticorrelation between the luminosity and the amplitude of the light curves of the quasars. For a sample of quasars, the more luminous are seen to vary over a smaller range of brightness than the less luminous ones.
Explanations to compensate for the lack of time dilation are discussed and involve the possibility that time dilation effects are exactly offset by an increase in the timescale of variations associated with black hole growth (thought to power the quasar), or that the variations that are observed are caused by microlensing,31 not intrinsic to the quasar, and hence, in such a case, time dilation would not be expected. But these would have to occur in the same manner over all timescales and are again a case of special pleading.
In the case of gravitationally lensed quasar images, there are some cases that seem to support the conventional redshift-distance relationship for quasars, e.g. QSO 0957+561;32 time variations/time delays between images of same source have been construed as supporting a standard value of the Hubble constant H0. However, Arp and others for a long time have argued that gravitationally imaged quasars may, in some cases at least, be pairs of quasars with very similar non-cosmological redshifts.7
GRB luminosity variations
Hawkins33 states that the evidence for time dilation from gamma ray bursts (GRBs) is inconclusive; initially because of the uncertainty in the intrinsic timescales of the bursts, and later, once the redshifts of bursts were found, the problem of correcting the raw data for selection effects involving an inverse correlation between luminosity and time measures made it difficult to use GRBs to detect time dilation.
However, Crawford34 finds that GRBs out to z = 6.6 show no evidence of time dilation in the raw data and he rejects the hypothesis with a probability of 4.4 × 10–6 that the data support the concept. He makes a careful analysis of the traditional explanation that an inverse correlation between luminosity and the time measures together with strong luminosity selection as a function of redshift cancels any observed time dilation. He confirms that there is an inverse correlation between luminosity and some time measures (there are four main ones, and it is strongly seen in two of them), but using the concordance cosmology strong luminosity selection cannot be achieved. It may be possible to explain the apparent lack of time dilation with a combination of gamma-ray-burst selection, some luminosity evolution and some time-measure evolution. But this requires a remarkable coincidence, where opposite effects exactly cancel, in order to produce the apparent lack of time dilation. However the data are consistent with a static cosmology in a non-expanding universe. He finds that, assuming a static universe, the total energy of the GRBs is invariant with redshift. This is a similar result that can be shown in the type 1a supernova data also.
Conclusion
A long time ago the Lord said through the prophet Isaiah,
“I made the earth and created man on it; it was my hands that stretched out the heavens, and I commanded all their host [emphasis added]” (Isaiah 45:12, ESV).
The Creator God made the heavens and set out all the stars and galaxies that we see in the night sky. Using this and several other verses like it, several creationists have contended that the Scriptures imply cosmological expansion of space. But that position cannot be justified from Scripture alone,35 Nor can it be concluded from this review of observational evidence.36
Scripture tells us,
“He hath made every thing beautiful in his time: also he hath set the world in their heart, so that no man can find out the work that God maketh from the beginning to the end [emphasis added]” (Eccl. 3:11, KJV).
From this passage it appears that there are those who cannot find out God’s Truth, possibly because they have rejected their Maker. They begin with the conclusion they seek. The universe formed itself in a big bang some 13.7 billion years ago and has expanded ever since. This is the basis on which they seek the answers to questions in the cosmos.
The best evidence in support of an expanding cosmos is the type 1a supernova observations. However, to choose the candidate supernovae, the standard concordance model is used. And yet those same observations can be made to fit a static universe without the time dilation factor necessary to the BB universe. In this case the main line of evidence in support of the big bang is the (1+z) time dilation factor, but if that is due to a selection effect, then there is no definitive evidence for an expansion as required. This paper has highlighted the lack of the necessary time dilation that should be present in an expanding universe. Part II of this paper details evidence against expansion.
References
- The Hubble law: recession speed of the galaxy is related to its distance, v = H0 r, where H0 is the Hubble constant. Return to text.
- It is not sufficient that a theory permits something to exist. Only experimental verification can establish some aspect of a theory to be correct. We are told that the Experimental Method looks to falsify a theory, but in reality a successful prediction establishes the idea. In cosmology this is not even possible, since we cannot interact with the only universe we have to experiment on. All we can do is provide a model and judge it by the statistics of how often we see the phenomena to occur etc. Return to text.
- Lieu, R., ΛCDM cosmology: how much suppression of credible evidence, and does the model really lead its competitors, using all evidence? 17 May 2007. Return to text.
- The mass density of the Universe expressed as a fraction of closure density where baryonic matter only comprises about 10% of the total mass. The rest is dark matter. Return to text.
- The dark energy density expressed as a fraction of closure density. Dark energy is related to the cosmological constant, a sort of anti-gravity driving the universe apart faster as time proceeds. Return to text.
- Hartnett, ‘Cosmology is not even astrophysics’, 3 December 2008. Return to text.
- Arp, H., Seeing Red, Redshifts, Cosmology and Academic Science, Apeiron, Montreal, 1998. Return to text.
- Hartnett, J.G., Quantized quasar redshifts in a creationist cosmology, J. Creation 18(2):105–113, 2004. Return to text.
- MacMillan, D.S., Quasar apparent proper motion observed by Geodetic VLBI Networks: in; Romney, J. and Reid, M. (Eds.), Future Directions in High Resolution Astronomy: The 10th Anniversary of the VLBA, ASP Conference Proceedings, vol. 340, Astronomical Society of the Pacific, San Francisco, pp. 477–481, 2005. Return to text.
- supernova.lbl.gov/public/. Return to text.
- www.cfa.harvard.edu/supernova//public.html. Return to text.
- Perlmutter, S. et al., Measurements of Omega and Lambda from 42 High-Redshift Supernovae, Astrophys. J. 517:565–586, 1999. Return to text.
- Marmet, L., On the interpretation of red-shifts: a quantitative comparison of red-shift mechanisms, www.marmet.org/cosmology/redshift/mechanisms.pdf, 24 April 2011. Return to text.
- Goldhaber, G., Groom, D.E., Kim, A. et al., Timescale stretch parametrization of type Ia supernova B-band light curves, Astrophys. J. 558:359–368, 2001. Return to text.
- López-Corredoira, M., Observational Cosmology: caveats and open questions in the standard model; in: Recent. Res. Devel. Astron. & Astrophys., vol. 1, pp. 561–587, 2003. Return to text.
- Crawford, D.F., Observational evidence favors a static universe, J. Cosmology, in press, 2011. Return to text.
- There is no reason why the mass of the white dwarf progenitor stars for these supernovae should increase as the universe ages, hence resulting in brighter explosions. One of the assumptions of the Cosmological Principle is that the physics of the universe is the same at all epochs. Return to text.
- Reiss, A. et al., Observational evidence from supernovae for an accelerating universe and a cosmological constant, Astron. J. 116: 1009–1038, 1998. Return to text.
- Turner, M.S., Dark matter and dark energy in the universe in the third Stromlo Symposium: the galactic halo, Astr. Soc. Pacif. Conf. Ser. 165:431, 1999. Return to text.
- Steinhardt, P.J. and Caldwell, R.R., Cosmic microwave background and large scale structure of the universe, Astr. Soc. Pacif. Conf. Ser. 151:13. 1998. Return to text.
- It cannot be determined without assuming a cosmological model first. Return to text.
- The Union data provided by Kowalski, M. et al., Improved cosmological constraints from new, old, and combined supernova data sets, Astrophys. J. 686:749–778, 2008. Return to text.
- Foley, R.J. et al., A definitive measurement of time dilation in the spectral evolution of the moderate-redshift type Ia supernova 1997ex, Astrophys. J. 626:L11-L14, 2005. Return to text.
- Aguirre, A. and Zoltan, A., Cosmological constant or intergalactic dust? constraints from the cosmic far-infrared background, Astrophys. J. 532:28–36, 2000. Return to text.
- Goobar, A., Bergström, L. and Mörtsell, E., Measuring the properties of extragalactic dust and implications for the Hubble diagram, Astron. & Astrophys. 384:1–10, 2002. Return to text.
- The metallicity in a source is the proportion of its matter made up of chemical elements other than hydrogen and helium. Since stars are composed mostly of hydrogen and helium, astronomers use for convenience the blanket term ‘metal’ to describe all other elements collectively. Return to text.
- Rowan-Robinson, M., Do type Ia supernovae prove L < 0?, MNRAS 332:352–360, 2002. Return to text.
- Ivanov, M.A., Possible manifestations of the graviton background, General Relativity and Gravitation 33:479–490, 2001; ERRATUM, 35:939–940, 2003; arxiv.org/PS_cache/astro-ph/pdf/0005/0005084v2.pdf. Return to text.
- Ivanov, M.A., No-time-dilation corrected Supernovae Ia and GRBs data and low-energy quantum gravity, Contribution to the VI Int. Workshop on the Dark side of the Universe (DSU2010), Guanajuato U., Leon, Mexico, 1–6 June 2010, ivanovma.narod.ru/no-time-dilation10.html. Return to text.
- Hawkins, M.R.S., Time dilation and quasar variability, Astrophys. J. 553:L97–L100, 2001. Return to text.
- When a quasar is sufficiently aligned with a massive compact foreground object the bending of light due to its gravitational field is distorted, resulting in an observable magnification. The timescale of the transient brightening depends on the mass of the foreground object as well as on the relative proper motion between the background ‘source’ and the foreground ‘lens’ object. Return to text.
- Walsh, D., Carswell, R.F. and Weymann, R.J., 0957 + 561 A, B: twin quasistellar objects or gravitational lens? Nature 279:381–384, 1979. Return to text.
- Hawkins, M.R.S., On time dilation in quasar light curves, MNRAS 405:1940–1946, 2010. Return to text.
- Crawford, D.F., No evidence of time dilation in Gamma-Ray Burst data, arxiv.org/PS_cache/arxiv/pdf/0901/0901.4169v1.pdf. Return to text.
- Hartnett, J.G., Does the Bible really describe expansion of the universe? J. Creation 25(2):125–127, 2011. Return to text.
- Occasionally I may update lines of evidence addressed in this paper and publish online at arxiv.org/PS_cache/arxiv/pdf/1107/1107.2485v1.pdf. Return to text.





Readers’ comments
Comments are automatically closed 14 days after publication.