Radiometric dating and the age of the Earth
[Click here for a summary of this article.]
Before 1955, ages for the Earth based on uranium/thorium/lead ratios were generally about a billion years younger than the currently popular 4.5 billion years. The radiometric evidence for a 4.5 b.y. old Earth is reviewed and deficiencies of the uranium/lead method are discussed. The basic theory of radiometric dating is briefly reviewed. Since 1955 the estimate for the age of the Earth has been based on the assumption that certain meteorite lead isotope ratios are equivalent to the primordial lead isotope ratios on Earth. In 1972 this assumption was shown to be highly questionable.
Despite this, the momentum gained in the two decades prior to 1972 has made 4.5 b.y. a popularly accepted “universal constant” even though the foundations on which it was based have been virtually removed. Some evidence is also presented to show that radiometric results that are in agreement with the accepted geological time scale are selectively published in preference to those results that are not in agreement.
Basics
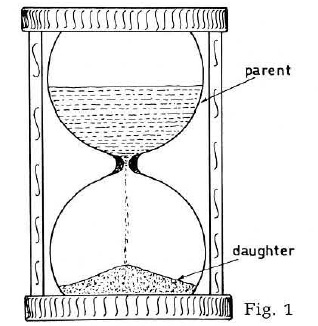
The geological time scale and an age for the Earth of 4.5 b.y. rely heavily on the uranium/thorium/lead radiometric dating methods.1,2,3 Because it is not generally appreciated that the assumptions on which the radiometric estimates are based are a virtually impossible sequence of events, let us refresh our minds on the fundamentals of the method by turning to the hourglass analogy (Fig. 1). This system of measuring time works well providing that:
- the hole does not clog up,
- the sand always flows at a known and reproducible rate,
- we know how much sand is in the bottom at the beginning,
- no sand is added or subtracted during the timing run. In other words, it has to be a closed system.
Since radioactive decay constants are believed to be unalterable, the requirement of an absolutely reproducible rate is hopefully met. Therefore, all one has to do in general terms is to find a radioactive mineral which has been a closed system since the time of mineralization, and for which the amount of the daughter product at the beginning is known, the so-called primordial amount, and the absolute age may be calculated from the present amount of parent and daughter isotopes in the mineral.
Briefly, the weakest points in this method are that (a) truly closed systems probably do not exist in nature,4 (b) the primordial concentration of isotopes is an intractable problem and the value chosen can only be based on assumptions and (c), even the invariance of decay constants is now under question.5,6,7,8,9,10,11,12

More than a dozen radioactive isotopes are known to have easily altered decay constants, by up to 4%13 by merely changing the chemical form of the isotope. Therefore, the following is simply a statement of the obvious;
“As in the case with radiometric ages determined from almost any rock unit it is impossible to establish unequivocally that the ages reported here reflect the time of original crystallization or emplacement of the bodies from which they are derived.”14
Before we consider the actual lead/lead isotope data there is one other comment that needs to be made regarding extrapolation of present rates. The radiometric dating method is basically an extrapolation of the form shown in Fig. 2.
If the decay constant is known with great accuracy, an extrapolation over one or two thousand years may be regarded as quite reasonable. An extrapolation over 5 b.y. is quite a different story. Five billion years is five million times greater than one thousand years. Therefore, if the extrapolation shown in Fig. 2 is 2.5 cm, five million times greater is about 125 km. It should be obvious that the further one projects present rates, the more likely one is to be quite wrong.
4.5 billion years
The 4.5 b.y. era started about 1955 with the publication of a classic paper by Patterson et al.2 In spite of cautions and scepticism advised by the authors this number has been widely and enthusiastically accepted and is usually quoted as if the evidence was decisive and conclusive. It has assumed something of the status of a universal constant to which all other data must be fitted, thus it has become common practice to assume that data which does not fit this result is either wrong or unintelligible.3
Now let us consider the actual lead/data from the extensive tabulations of Faul15 and Russell and Farquhar.16 The following analysis is given in the book Prehistory and Earth Models by Melvin Cook.17 A reproduction of the data is shown in Fig. 3.
Lead-206 and lead-207 are known daughter products from the decay of uranium-238 and uranium-235, respectively. Lead-204, a minor isotope of common lead, has no radioactive parent and is believed to be primordial lead. Lead-206 and lead-207 are also believed to be present in primordial lead since there is insufficient uranium to account for all the lead. Just how much lead-206 and 207 were present at the beginning, nobody knows. Any amounts chosen must be based on assumption.
As a uranium ore ages, the ratio of lead-206 to lead-204 increases as does the ratio of lead-206 to lead-207. These ratios for many lead ores are plotted in Fig. 3. The lowest ratios are taken to be the most ancient ores, formed at the beginning, billions of years ago and separated from further radiogenic enrichment.
Higher ratios are formed as the lead is fed by ageing uranium ore bodies. The theoretical limit to a 4.5 b.y. old lead fed continuously by uranium occurs at a lead-206 to lead-204 ratio of 18.5, which is taken as the present ratio for common lead. This limit is shown in Fig. 317 as the upper boundary to the time clock zone.
One third of lead ores are regarded as anomalous,17,18 since they have negative ages, that is, ages extending billions of years into the future, in some cases. These are shown in Fig. 3 as the alteration zone. They show that widespread contamination and differentiation from various sources of lead have occurred during the more than one thousandfold concentration into the present lead ore deposits.19

The main problem is this. There is no discontinuity whatever between results lying in the time clock zone and those lying in the alteration zone. All the data show the same scatter.
Since there is no reason why the alteration zone should not extend into what is classified as the time clock zone (apart from a belief in 4.5 b.y.), the majority of the data can be explained as indicating a history of geochemical alteration. Therefore the ores lying in the time clock zone are not necessarily any more a reflection of age than those lying in the alteration zone and ones lying in the alteration zone cannot possibly be time indicators.
It is probably because of this type of evidence for extensive mixing in the alteration zone that Patterson et al.2 were highly critical of the lead ore method of dating.
They wrote:
“In view of the evidence for extensive mixing, it would seem contrary to the facts to postulate differing frozen lead/uranium ratios that have existed for billions of years. The requirements of the assumptions in the lead ore method are so extreme it is unlikely that it should give a correct age.”
So they took a different approach. They estimated the age of the Earth by substituting the lead isotope ratios of certain meteorites in the Holmes-Houtermans equation. In this equation the primordial lead ratios are required. The values they assumed were based on the lead isotope ratios observed for three meteorites.
Since meteorites have not proved to be the ancient objects from the sky that one might imagine,20 it is surprising that they should be assumed to give the primordial lead composition on Earth. That difficulty aside, they were selected because they contain very little uranium and thorium and are therefore unlikely to contain significant radiogenic lead. However, it is even more surprising to learn that the lead isotope ratios chosen by Patterson et al.2 have been found to be not representative of the majority of meteorites.21
Most meteorites have lead isotope ratios similar to those of present day common lead. Up until 1972 these could be explained as being contaminated with radiogenic lead from uranium and thorium decay. In 1972, however, Gale et al.22 showed unequivocally that there is by no means sufficient uranium and thorium to account for what could previously have been called radiogenic lead. Since the lead in meteorites can no longer be ascribed to uranium/thorium decay, it may also be taken to represent primordial lead.
Therefore, since the lead isotope ratios for the majority of meteorites are the same as present day common lead ratios and may also be assumed to represent primordial lead, the billion year age chronology disappears.
In case the significance of these results is ignored, a few sentences from the Gale et al.22 should reveal their importance:
“ … it is not widely appreciated, outside the ranks of those who work directly in geochronology or meteoritics that, judged by modern standards, the meteoritic lead-lead isochron is very poorly established.
“This (work) shows unequivocally for the first time that there is indeed a real problem in the uranium/lead evolution in meteorites, in that in each of these meteorites there is now insufficient uranium to support the lead isotope composition.
“It therefore follows that the whole of the classical interpretation of the meteorite lead isotope data is in doubt, and that the radiometric estimates of the age of the Earth are placed in jeopardy.”
In plain language, the radiometric estimates for the age of the earth are lacking real foundations.
Concordant data
It might be argued that although radiometric dating has a few problems, the large body of concordant data using different isotopes shows that the dates are of the right order. In fact, there is no large body of concordant data. There is a large body of discordant data but concordant data are scarce. In 1955 a symposium on radiometric dating was held from which the following was given in the summary:23
“Radioactive ‘dating’ has been perhaps the most widely publicised of geochemical techniques, but of several known dating methods based on radioactivity, only C-14 dating has developed to the point where it yields consistently reliable ages. Mineral ages obtained from isotope ratios like Pb-206/ U-238, Pb-207/ U-235, and Pb-207/Pb-206, for instance, usually do not agree.”
By 1965 the situation had grown no better:24
“Mr Webster Smith … regarded the atomic dating method (except in respect to carbon) as still very tentative especially where the older rocks were concerned and where discordant and even absurd results were quite common. There were records of granites which atomically were older than other granites that they intruded … argon was all too prone to be either deficient, wholly absent, or even too high; in such cases the author ‘adjusted’ his figures.”
By 1976 still no improvement had emerged as the following quotation from even the most general of scientific references, the Encyclopedia Britannica shows:25
“Unfortunately, such checks have painted a generally gloomy picture for those seeking a chronometric tool … Experience shows that, with the exception of results from the mineral uraninite, the three uranium-thorium-lead ages are almost always different.”
Where comparison has been possible, the rubidium/strontium age is usually much greater than the uranium/lead age or the lead/lead age.26 The potassium/argon age is likewise generally different from other isotopic ages. It has been pointed out by Cook27 that there is about ten times more strontium-87 than could arise from rubidium-87 decay alone even if the Earth were 4.5 b.y. old. That is, about 90% of the strontium-87 must be primordial even on the basis of rubidium-87 decay for 4.5 b.y. It has been similarly shown that there is not nearly enough potassium-40 to account for all the argon-40.28 It therefore seems quite likely that strontium-87 and argon-40 counted as radiogenic are actually primordial. Any decrease in the assumed radiogenic component, however, shortens geological time.
Selective data publication
Is there any significance therefore in the rough correlation between some radiometric dates and ages assigned to the geological column? A rough correlation of results is to be expected if publication of ‘agreeable dates’ occurs selectively over grossly discordant dates, and such selective publishing is freely admitted to be a common practice:
“In general, dates in the ‘correct ball park’ are assumed to be correct and are published, but those in disagreement with other data are seldom published nor are discrepancies fully explained.”29
“Unpublished work by the author on Silurian shales from Pembrokeshire and the Welsh Borderlands has shown that such rocks can define isochrons giving ages significantly younger than the time of deposition adduced from faunal evidence.”30
“In conventional interpretations of K/Ar age data, it is common to discard ages which are substantially too high or too low compared with the rest of the group or with other available data, such as the geological time scale. The discrepancies between the rejected and the accepted are arbitrarily attributed to excess or loss of argon.”31
The following quotation from Houtermans32 may show the pressure to conform to the accepted time scale:
“Sometimes the dates given by radioactive methods are accepted enthusiastically by the classical geologists, sometimes if these dates do not fit their previously formed hypotheses they come to the conclusion to deny the usefulness of radioactive methods altogether.”
In a recent article in Science, entitled “Timekeepers of the Solar System”33, leading rock-dater Wasserburger is reported to have said:
“We’re building a new generation of fairy castles and myths for the next generation to play with.”
That is a perfectly realistic assessment of radiometric rock dating methods, and serious chronologists should prefer something more than fairy castles.
Henry Faul in his book Ages of Rocks, Planets and Stars34 stated:
“Much geologic insight into the origin and history of ores can be gained from judicious interpretation of the isotopic composition of lead, but colossal misconceptions can arise from false assumptions.”
The key word used by Faul is “judicious” and in context implies interpretation in conformity with the accepted geological time scale. The assumption of a great age will influence the interpretation of the data and is certainly likely to lead to colossal misconceptions, the most outstanding of which is the widely propagated view that radiometric dating has established the age of the Earth to be 4.5 b.y.
Acknowledgements
The author received considerable help from the ICR technical monograph on radiometric dating by Prof. H. Slusher, and the extensive documentation provided by J. Woodmorappe in the CRS Quarterly.35 He also acknowledges valuable material supplied in correspondence with Drs. R. Kofahl, J. Read, and H. Slusher.
References and notes
- Faul, H., Nuclear Geology, John Wiley & Sons Inc., New York, p. 257, 1954. Return to text.
- Patterson, C., Tilton, G. and Inghram, M., Science 121:69, 1955. Return to text.
- The outstanding example of this is the rejection of all geochronometers that indicate a significantly younger age than 4.5 b.y. Return to text.
- Faul, ref. 1, p. 18. Return to text.
- Dudley, H.C., The Morality of Nuclear Planning, Kronos Press in association with the centres of Interdisciplinary Studies, Glassboro State College, Glassboro, New Jersey, p. 61, 1976. Return to text.
- Dudley, H.C., Chem. and Eng. News, p. 2, 7 April 1975. Return to text.
- Read, J., Chem. and Eng. News, p. 5, 14 July 1975. Return to text.
- Pauling, L., ibid. Return to text.
- Emery, C.T., Ann. Rev. Nuclear Science 22:165, 1972. Return to text.
- Anderson, J.L., J. Phys. Chem. 76:3603, 1972. Return to text.
- Anderson, J.L. and Spangler, C.W., J. Phys. Chem. 77:3114, 1973. Return to text.
- Hahn. H,-P., Born, H.-J. and Kim, J.I., Radiochimica Acta 23:23, 1976. Return to text.
- Decay constants would need to vary by much more than 4% to affect radiometric dating significantly if the decay constant were the only unknown. However, the fact that decay constants have not even been measured for a period of one hundred years and the fact that the phenomenon of radioactive decay is not perfectly understood shows what an extreme assumption is involved in extrapolating these ‘constants’ for ten thousand years, let alone millions of years. Return to text.
- Barton Jr, I.M., Canad. J. Earth Sciences 14:1641, 1977. Return to text.
- Faul, ref. 1, p. 264. Return to text.
- Russell, R.D. and Farquhar, R.M., Lead Isotopes in Geology, Interscience Publishers, New York, 1960. Return to text.
- Cook, M.A., Prehistory and Earth Models, Max Parrish, London, p. 44, 1966. Return to text.
- Faul, ref. 1, p. 298. Return to text.
- Cook, ref. 16, p. 37. Return to text.
- Faul, H., Ages of Rocks, Planets and Stars, McGraw-Hill Book Co., p. 75, 1966. Return to text.
- Faul, ref. 19, p. 74. Return to text.
- Gale. N.H., Arden, J. and Hutchison, R., Nature Phys. Science 240:57, 1972. Return to text.
- Summary of an Amer. Chem. Soc. symposium, Chem. and Eng, News, p. 330, 23 January 1956. Return to text.
- Sabine, P.A. and Watson, J.J., Geol. Soc. London 12:525, 1965. Return to text.
- Encyclopedia Britannica, Vol. 5, p. 505, 1976. Return to text.
- Faul, ref. 1, p. 256. Return to text.
- Cook, ref. 16, p. 64. Return to text.
- Cook, ref. 16, p. 66. Return to text.
- Mauger, R.L., Contributions to Geology 15:37, 1977. Return to text.
- Bath, A.H., J. Geolog. Soc. London 130:570, 1974. Return to text.
- Hayalsu, A., Canad. J. Earth Sciences 16:974, 1979. Return to text.
- Houtermans, F.G., The Physical Principles of Geochronology, Colloques Internationaux du Centre National de la Recherche Scientifique No. 151, p. 242, 1966. Return to text.
- Science, p. 55, May/June 1980. What is not said in this article is that other ages ranging from 2 to 28 b.y. have been obtained. Return to text.
- Faul, ref. 19, p. 69. Return to text.
- Woodmorappe, J., Creation Research Society Quarterly 16:102, 1979. Return to text.




Readers’ comments
Comments are automatically closed 14 days after publication.