Journal of Creation 32(2):124–127, August 2018
Browse our latest digital issue Subscribe
Effective population sizes and loss of diversity during the Flood bottleneck
The extreme population bottleneck that occurred during the biblical Flood should have caused a loss of human genetic diversity. According to Scripture, the entire world population was reduced to three reproducing couples. The maximum effective population size of the Ark-borne population was calculated to be 4.75 individuals (carrying the equivalent of 9.5 haploid genomes). What effect would this have had on allelic diversity today? How much ‘created diversity’ would have been lost? The HapMap data was used to estimate the number of people required to capture X percent of the pre-Flood diversity. Even though it would require an average of 61 people to capture 99% of current diversity, the Ark passengers could have carried nearly 80% of the then-circulating alleles. Also, pre-Flood mutations were more likely to have been lost than created alleles. Even so, over 20% of created alleles should have been lost. This could have played a role in the approximately 90% decline in lifespan between the antediluvian Patriarchs and today, although one would not expect a continuing decline in diversity because the rapid expansion of the post-Flood population would have cancelled out most of the effects of genetic drift.

There were eight passengers on the Ark, but there were not eight founders of the post-Flood population. Not only are no additional children recorded for Noah and his wife, but Genesis 9:18–19 specifically claims that Shem, Ham, and Japheth are the ancestors of the “people of the whole earth”. But since the three founding males were all brothers, we need to take an inbreeding coefficient into account. This would have reduced the ‘effective’ population size to less than six people.1
People carry two haploid copies of the human genome. Due to chromosomal recombination, any portion of either copy has a probability of inheritance of ½ per child. Thus, the three brothers combined do not equate to six haploid genomes, because their parents only carried four haploid genomes between them. Yet, since they represented a subsampling of the four haploid genomes of their parents, portions of the genomes of Noah and his wife may have been lost.
For any given heterozygous allele, there is a 25% probability that only one of the two alleles will be passed by one of the parents to all three sons (table 1). In these cases, the alternate allele is lost forever. Thus, approximately ¼ of Noah’s allelic diversity and ¼ of his wife’s allelic diversity should have been lost. You can see evidence of this in the various plots of Carter and Powell (cf. figure 2a–d).2 Instead of carrying the entire genome of both Noah and his wife, the brothers carried only 75% of each. In the end, Shem, Ham, and Japheth equate to only 1.5 people. Thus, the effective population size on the Ark was, at most, 3 + 2 – (0.53× 2), or 4.75 people.

However, if the three daughters-in-law are closely related, to each other or to the three brothers, the inbreeding coefficient will be even stronger, and the effective population size will be that much lower. If the daughters-in-law are actual daughters (sisters to the three brothers), only the genomes of Noah and his wife could possibly have made it through the Flood. But, some small portion of their genetic diversity would still have been lost, despite the six-fold sampling. The effective population size in this case would be 2 – (0.56× 2) =1.96875.
Other cases, such as where the daughters-in-law were grandchildren, are possible, but the above two scenarios show the maximum and approximate minimum bounds. We do not know the true value, but I am hoping that some enterprising creation scientist will take up the challenge. The evidence should reside in the human genome.
For the purposes of the current study, it is clear that some allelic diversity should have been lost during the Flood. But how much would be lost? How much of the antediluvian genetic diversity did the Flood bottleneck wipe out if there was an effective population size of only 4.75 individuals on the Ark? Would the bottleneck have produced catastrophic levels of inbreeding?
The HapMap database can be used to answer questions like these. It was designed to sample a significant fraction of the most common genetic variants carried by modern humans. To that end, they sequenced 1.6 million single letters scattered throughout the genomes of 1,301 people from 11 diverse world populations. The sampling strategy was designed to cover approximately 10% of the total diversity found in the human genome, and there was an average of less than 2,000 nucleotides between the variants they sampled.3 The HapMap Project has been mostly superseded by larger genomics programs like the completed 1,000 Genomes Project4 or the upcoming 100,000 Genomes (UK) and 1,000,000 Genomes (US) efforts. However, the original HapMap data are excellent for the purposes of elucidating multiple aspects of the genetics of creation.

First, the data are almost all bi-allelic. That is, only two alleles exist for almost all data points (i.e. A or T, G or C). This makes for simpler historical reconstructions. Second, the data are dense, meaning they covered most of the genome with deep enough sampling to allow us to draw multiple significant conclusions about human history. And, since the sampled locations effectively cover the entire genome, we can use the data as a proxy for genome-wide processes and statistics. Third, they only sampled single-nucleotide polymorphisms (SNPs). A polymorphism is defined as an allele with a frequency of at least 0.01 in the population. Since new mutations always start out rare, with a frequency of 1⁄2n by definition,5 a polymorphism is more likely to be in the ‘created’ category. Fourth, they preselected variants that are found across the world. Since it would be statistically impossible for millions of mutations to appear independently in multiple separate populations, bi-allelic SNPs with a worldwide distribution are strong candidates for ‘created diversity’.
Methods
The HapMap phase 3 (release 2) data were downloaded from the HapMap Project website (ftp://ftp.ncbi.nlm.nih.gov/hapmap/). The data for each population are contained in two files. The first is a ‘MAP’ that consisted of a simple ordered list of SNPs, the SNP name (if previously described), the chromosome on which the SNP is located, and its position (in nucleotides) along the chromosome. The ‘PED’ file contains sequencing data for each individual in the population. Since humans carry two of each autosome, any genomic location can contain up to two letters. Sequences were thus reported in ordered pairs (A/A, C/T, G/C, etc.). The order of SNPs in the MAP files corresponds to the data columns in the PED file. Using that information, I took the autosomal data and stripped out all SNPs that were not reported in all 11 populations or that were invariant in one or more populations, leaving 995,358 SNPs. I next calculated the allele frequencies for each allele of each SNP in each population. Some of the populations were sampled in 2-parent-child trios (table 2), so care had to be taken when calculating allele frequency; for example, not to include the children.

Next, since the individuals were not ordered according to relationship, I took the population data files and calculated the proportion of SNPs that were contained in n individuals (figure 1), starting with the first individual in the file and adding the other individuals in the order given. In any population-wide sampling scheme, one would expect to uncover a few cryptic relationships (cousins, aunts, uncles, etc.). However, for the purposes of this step, these can be ignored. The inclusion of closely related individuals early in the process could affect the results, but this should show up as a dip in the curve. Also, any effect will be averaged out quickly as distantly related people are added.
While I was calculating the above statistics, I included the average frequency of the SNPs not contained in n individuals. This tells us the degree to which rare alleles are disfavoured during the bottleneck.
Results

Across all 11 populations, a single individual carried an average of 31.1% (± 0.005 SD) of the allelic diversity. It required a minimum of 21 individuals to carry 95% of worldwide SNP diversity and 57 individuals to carry 99% (table 3). This is far greater than the effective population size during the Flood. However, even the minimum values for the effective population size during the Flood would have captured a significant proportion of the pre-Flood diversity (figure 1). By interpolation, with an effective population size of only 4.75 people the Ark passengers could easily have contained up to 77.3% of the then-circulating alleles. In the worst-case scenario, with an effective population size slightly less than 2.0, approximately 57.355% of all created alleles would be expected to have been captured. And, using any modern population as a proxy for the pre-Flood world would produce similar results (figure 2).
Discussion
If we wish to know if the biblical Creation–Flood–Babel model is realistic, we need to evaluate the percentage of the antediluvian allelic diversity that could have been carried by the Ark passengers. The majority of created diversity alleles should have been on the Ark. Even though it would require dozens of people to capture 95% or more of the pre-Flood diversity, the Ark passengers would have captured at least the majority of alleles even in the worst-case scenarios. Rounding off, we can conclude that on the order of 60–80% of pre-Flood diversity should have been retained through the Flood.
Since mutations, by definition, always enter the population at a frequency of 1⁄2n, and since nearly all new mutations are lost to drift within a few generations,6 mutations are almost always rare. It would take strong selection, extreme levels of genetic drift during a long and narrow bottleneck, or vast periods of time to drive most mutations to any appreciable frequency. Due to the fact that rare alleles were less likely to have been captured by the Ark passengers, pre-Flood mutations were more likely to have been lost than created alleles.
Alternatively, depending on initial conditions, created alleles should have started off at a high frequency. In the simplest model, God created Adam’s genome with millions of heterozygous alleles. Any variation that Adam carried would have had an initial frequency of 0.5. Since Eve was manufactured from Adam’s flesh, a simplifying assumption is that she would have carried any heterozygous sites he did, with the exception of Adam’s Y chromosome, while Adam’s X chromosome would have been doubled in Eve. An alternate model has Eve being a haploid clone of Adam, meaning all alleles start out at a frequency of 0.75, 0.5, or 0.25. There are other, more complex models where, for instance, God engineered multiple different genomes into the reproductive cells of both Adam and Eve. All people who came after Adam and Eve (with the exception of Jesus) had to have been produced by normal sexual reproduction, but there is really no limit to the amount of diversity that could have been front-loaded into Adam and Eve. In this case, the allelic diversity of the pre-Flood world would have depended on how many children they had.
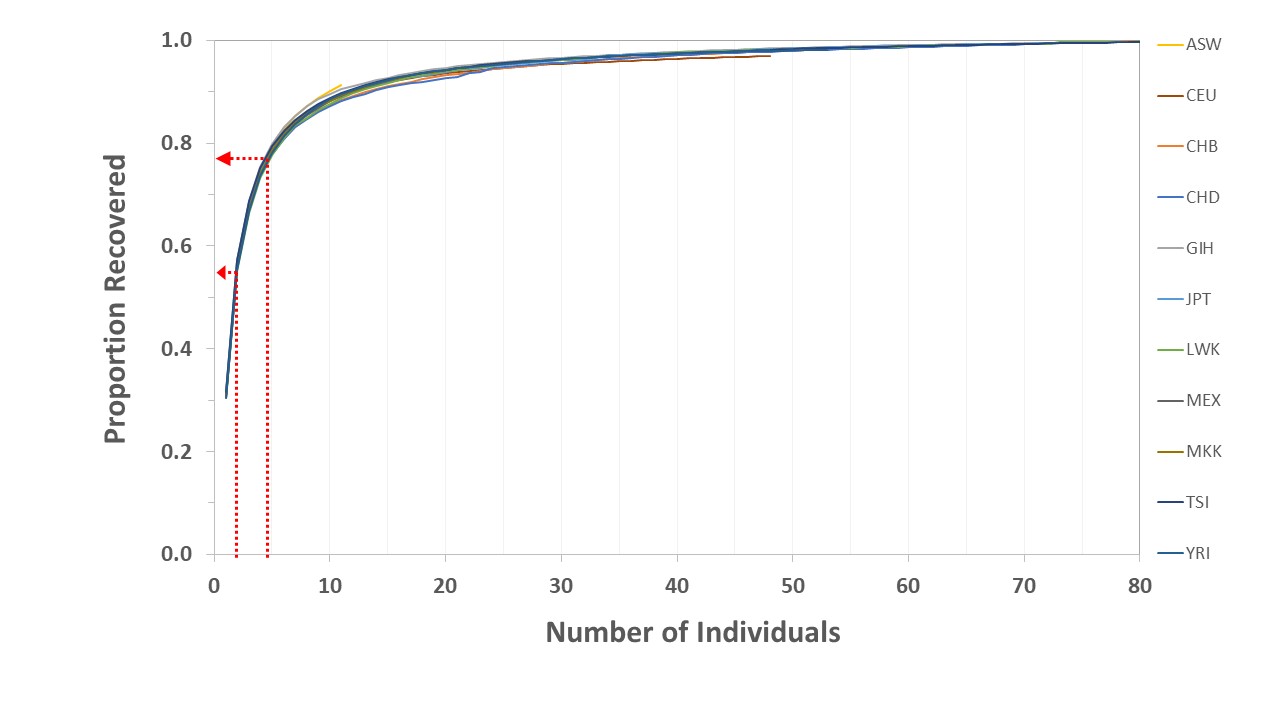
But exotic models, however interesting, are probably not needed. If the average person alive today carries approximately ⅓ of all the common alleles in the world (figures 1 and 2), it would not be a stretch for God to have put those alleles right into the founding couple. And, since the most common alleles are generally not disease-causing,7 this level of heterozygosity should not have been harmful.
Also, from the data presented here, it is clear that common alleles were more likely to have been captured. This is something that Woodmorappe noticed more than 20 years ago,8 but here I quantify it more clearly. The Flood, instead of having a negative effect, would have removed a good deal of the antediluvian mutation burden, to the extent that it existed. Some of the remaining mutations could have drifted to higher frequencies during the post-Flood population rebound,2but the number should not have been extreme.
More than 20% of created diversity should have been lost. Did this have an effect on human phenotypic diversity, lifespan, or intelligence? Perhaps, but rapid post-Flood population growth should have prevented further loss of genetic diversity. Populations in exponential growth generally do not undergo genetic drift, especially after reaching a size of a few hundred individuals.2 In the end, we can see the effects of the Flood bottleneck. It would have removed some of the pre-Flood diversity. That is impossible to ignore. However, most of the diversity, especially most of the created diversity, should have made it through the bottleneck and, thus, should still be around today.
References and notes
- The terms ‘effective population size’ and ‘inbreeding coefficient’ are used here in a slightly different sense than the standard use among population geneticists. Technically, effective population size is defined as the number of individuals in a population that contribute offspring to the next generation. However, it is usually back-calculated from genetic data (as in, “How many individuals would be required to carry the diversity we see in the population today?”), as they rarely know exactly how many individuals in a population sire offspring at any point in time. The inbreeding coefficient is technically defined as the probability that any variant carried by two individuals and chosen at random will be identical by descent. In other words, the probability they carry the same stretch of DNA because it was mutually inherited from a common ancestor. In both cases the phrases are technically used correctly, even if most population geneticists would not think to apply them to biblical scenarios. Return to text.
- Carter, R.W. and Powell, M., The genetic effects of the population bottleneck associated with the Genesis Flood, J. Creation 30(2):102–111, 2016. Return to text.
- The International HapMap 3 Consortium, Integrating common and rare genetic variation in diverse human populations, Nature 467(7311):52–58, 2010 | doi:10.1038/nature09298. Return to text.
- The 1000 Genomes Project Consortium, An integrated map of genetic variation from 1,092 human genomes, Nature 491(7422):56–65, 2012 | doi:10.1038/nature11632. Return to text.
- This formula is simply a product of the population size (n) and the fact that there are two copies of each chromosome in each individual. Mutations appear mostly as copying errors in one of the chromosomal copies, hence their starting frequency is always 1/2n. Return to text.
- Rupe, C.L. and Sanford, J.C., Using numerical simulation to better understand fixation rates, and establishment of a new principle: Haldane’s Ratchet, Proceedings of the Seventh International Conference on Creationism, Creation Science Fellowship, Pittsburgh, PA, 2013. Return to text.
- The most common alleles are generally not disease-causing. A basic expectation of evolutionary theory is that selection should act to reduce the frequency of disease-causing alleles over time. However, this is also borne out in multiple genetic studies, e.g. the great majority of the 1.3 million alleles sampled by the HapMap Project are not associated with disease phenotypes. Most creation models would assume all ‘created diversity’ alleles would not be deleterious while perhaps many post-creation mutations would be. Return to text.
- Woodmorappe, J., Noah’s Ark: A feasibility study, Institute for Creation Research, Santee, CA, pp. 192–195, 1996. Return to text.




Readers’ comments
Comments are automatically closed 14 days after publication.